exp(3-4/5)+ sqrt(3+2^5)/(4-7*log(10))[1] 8.536811Soluzioni esercizi
Lab 1
Esercizio 1
- Calcolare \(\exp(3-\frac{4}{5})+\frac{\sqrt{3+2^5}}{4-7\cdot \log(10))}\)
- Creare il vettore
xcontenente i valori \((10, log(0.2), 6/7, exp(4), sqrt(54), -0.124)\):
- Determinare la lunghezza di
x.
x = c(10, log(0.2), 6/7, exp(4), sqrt(54), -0.124)
x[1] 10.0000000 -1.6094379 0.8571429 54.5981500 7.3484692 -0.1240000length(x)[1] 6sum(x)[1] 71.07032Esercizio 2
- Commentare ogni riga del seguente codice spiegando quale operazione viene eseguita.
x = c(3,6,8)
x
x/2
x^2
sqrt(x)
sum(x)x = c(3,6,8) #creo un vettore di 3 elementi
x #visualizzazione dell'oggetto x[1] 3 6 8x/2 #ogni elemento di x è diviso per 2 (si ottiene un nuovo vettore)[1] 1.5 3.0 4.0x^2 #ogni elemento di x è elevato alla seconda (si ottiene un nuovo vettore)[1] 9 36 64sqrt(x) #per ogni elemento di x si calcola la radice quadrata (si ottiene un nuovo vettore)[1] 1.732051 2.449490 2.828427sum(x) #si sommando i valori di x (si ottiene un numero)[1] 17mean(x) #si calcola la media dei valori di x (si ottiene un numero)[1] 5.666667sum(log(sqrt(x))) #prima calcolo sqrt dei valori di x, poi log e ottengo un vettore di cui calcolo la somma[1] 2.484907y = x #creo una copia di x che si chiama y
z = x+3*y^2 # creo un nuovo oggetto i cui elementi sono dati da una trasformazione dei elementi di x e yLab 2
Esercizio 1
Si considerino nuovamente i dati disponibili nel file DatiRegioni.csv.
dati <- read.csv("./data/DatiRegioni.csv", stringsAsFactors = T)Calcolare quanto segue: 1. il totale della popolazione residente in Italia.
sum(dati$pop)[1] 58997201- la superficie totale dell’Italia.
sum(dati$superf) #kmq[1] 302068.2- Il numero medio e mediano di abitanti per regione. Interpretare i valori.
mean(dati$pop)[1] 2949860# in ogni regione sono residenti in media circa 3 milioni di persone
median(dati$pop)[1] 1712378# almeno il 50% delle regioni ha un numero di residenti <= 1712378
# almeno il 50% delle regioni ha un numero di residenti >= 1712378- La superficie media e mediana per regione. Interpretare i valori.
mean(dati$superf)[1] 15103.41# la superficie media di ogni regione è di circa 15000 kmq
median(dati$superf)[1] 14446.1# almeno il 50% delle regioni ha una superficie <= 14446.1
# almeno il 50% delle regioni ha una superficie >= 14446.1Esercizio 2
Si consideri il file Excel Classificazioni statistiche-e-dimensione-dei-comuni_31_12_2023.xlsx fornito da Istat.
I punti da 1. a 4. sono svolti esternamente a RStudio.
- Importare il file in RStudio creando un oggetto di nome
daticom(ignorare gli eventuali messaggi di warning dovuti ai comuni con nome accentato). Quante righe e quante colonne ha il dataframe?
daticom <- read.csv("./Data/DatiCom.csv", comment.char="#", stringsAsFactors=TRUE)
nrow(daticom)[1] 7900ncol(daticom)[1] 11- Controllare la natura delle variabili nel dataframe
daticom(in base alla loro conoscenza preliminare).
str(daticom)'data.frame': 7900 obs. of 11 variables:
$ codreg : int 1 1 1 1 1 1 1 1 1 1 ...
$ codcom : int 1001 1002 1003 1004 1006 1007 1008 1009 1010 1011 ...
$ nomecom : Factor w/ 7895 levels "Abano Terme",..: 61 86 92 121 168 172 173 230 234 246 ...
$ sup : num 13.2 15.7 46.3 11.7 17.9 ...
$ pop : int 2558 3681 465 1628 6280 251 16497 2012 479 810 ...
$ zona_alt: int 3 5 1 3 3 1 3 3 1 1 ...
$ alt : int 315 257 1080 230 364 957 314 306 836 782 ...
$ lito : int 0 0 0 0 0 0 0 0 0 0 ...
$ isol : int 0 0 0 0 0 0 0 0 0 0 ...
$ cost : int 0 0 0 0 0 0 0 0 0 0 ...
$ urban : int 2 3 3 3 2 3 2 3 3 3 ...- Ricavare la distribuzione di frequenza della variabile
codreg(eventualmente vedere qui per i nomi e codici delle regioni). Calcolare, se possibile, la moda, la media e la mediana.
# numero di comuni per ogni regione
table(daticom$codreg)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1180 74 1503 282 563 215 234 330 273 92 225 378 305 136 550 257
17 18 19 20
131 404 391 377 # la regione con più comuni (la moda) è la numero 3 (Lombardia)
# non è possibile calcolare media e mediana- Ricavare la distribuzione di frequenza della variabile
zona_alt(anche includendo le frequenze percentuali). Calcolare, se possibile, la moda, la media e la mediana.
table(daticom$zona_alt)
1 2 3 4 5
2370 117 2530 785 2098 table(daticom$zona_alt)/nrow(daticom)*100
1 2 3 4 5
30.000000 1.481013 32.025316 9.936709 26.556962 # la moda è la modalità 3 (collina interna)
# non è possibile calcolare media e mediana- Ricavare la distribuzione di frequenza della variabile
alt. Calcolare, se possibile, la moda, la media e la mediana. Calcolare inoltre l’altitudine minima e massima.
table(daticom$alt)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
3 12 39 34 32 51 42 38 32 32 43 27 34 22 16 28
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
34 16 24 24 22 21 29 19 21 29 19 11 20 20 25 19
32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
15 12 16 16 23 10 12 10 17 4 23 18 23 17 10 16
48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
14 10 17 9 11 9 10 15 18 11 12 11 20 10 10 9
64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
13 17 12 20 21 9 19 8 15 14 19 25 19 16 20 10
80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
23 7 9 18 14 14 18 9 14 13 21 13 9 12 4 12
96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111
14 20 15 10 12 12 14 12 12 15 12 13 12 11 14 8
112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127
15 8 9 14 9 8 13 10 13 17 12 11 9 17 8 7
128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143
10 11 21 9 11 10 9 12 8 8 7 3 19 9 11 6
144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159
12 10 6 11 7 10 12 8 12 6 13 10 9 10 10 7
160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175
10 14 12 5 4 15 7 5 5 7 21 7 6 5 3 14
176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191
10 12 6 9 15 3 8 6 8 7 9 14 5 8 16 10
192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207
11 7 13 8 8 12 7 16 31 10 15 12 15 15 11 8
208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223
8 8 25 10 8 8 11 14 20 7 12 16 14 7 10 7
224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239
11 27 10 12 5 11 19 13 13 10 12 14 11 13 4 7
240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255
23 11 7 13 6 8 10 17 6 12 33 10 10 11 11 11
256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271
11 18 11 2 26 13 19 10 10 18 7 16 13 2 26 11
272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287
16 20 12 29 14 12 7 8 28 12 8 11 9 12 5 13
288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303
8 12 22 6 10 11 9 11 13 8 5 10 49 10 5 11
304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319
13 13 6 13 5 6 20 2 6 8 9 11 6 12 6 9
320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335
26 15 10 6 5 15 7 10 15 11 19 6 7 8 12 8
336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351
6 7 6 2 13 9 15 10 6 11 6 3 7 8 31 7
352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367
9 6 6 10 11 7 10 6 24 3 5 9 10 11 6 5
368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383
8 10 17 6 9 2 6 14 9 5 7 5 18 8 7 10
384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399
5 15 6 5 6 3 18 11 4 7 10 5 5 9 11 5
400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415
34 4 5 5 8 17 9 3 6 8 18 5 10 4 11 10
416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431
8 9 3 7 36 7 3 7 7 20 7 6 10 11 22 8
432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447
9 4 3 3 6 4 5 2 6 10 3 3 7 9 6 7
448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463
6 3 40 4 5 4 7 5 6 7 5 8 20 5 1 4
464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479
3 12 2 4 8 4 15 5 8 5 4 18 6 2 4 7
480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495
20 5 11 5 4 9 5 3 2 2 10 5 3 5 4 8
496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511
8 4 1 4 25 4 8 5 8 4 5 4 7 5 10 5
512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527
4 5 5 11 11 6 3 6 22 8 5 9 2 9 5 1
528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543
4 4 19 5 4 5 4 6 6 2 2 4 20 2 3 3
544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559
2 5 4 4 4 9 24 3 8 2 7 5 3 4 8 6
560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575
16 3 3 5 5 7 5 6 7 2 10 3 3 2 3 14
576 577 578 579 580 581 582 583 585 586 587 588 589 590 591 592
5 2 3 2 6 6 5 1 5 5 3 5 3 11 3 2
593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608
2 5 6 3 2 1 2 24 2 8 3 8 3 7 5 6
609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624
2 8 3 4 4 4 7 4 2 3 4 13 5 3 2 1
625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640
15 5 2 3 4 19 2 3 2 2 6 3 2 2 4 15
641 642 644 645 646 647 648 649 650 651 652 653 654 655 656 657
3 2 4 3 5 5 7 4 30 3 5 3 5 7 3 3
658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673
6 5 12 6 4 3 6 3 7 3 4 4 7 4 4 2
674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689
3 5 4 1 4 3 11 2 5 3 3 4 3 3 2 4
690 691 692 694 695 696 697 698 699 700 701 702 703 704 705 706
8 7 4 1 3 3 7 4 2 16 1 1 3 4 5 2
707 708 710 711 712 713 714 715 716 718 719 720 721 722 723 724
1 1 13 3 1 1 7 3 2 1 3 11 10 1 3 4
725 726 727 728 729 730 731 732 734 735 736 737 738 739 740 741
8 4 1 5 1 15 1 9 3 7 2 3 4 1 13 2
742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757
4 3 5 5 1 1 2 2 21 4 3 3 2 4 6 6
758 759 760 761 762 763 765 766 767 768 769 770 771 772 773 774
4 1 8 2 3 1 4 4 2 1 4 5 3 4 1 3
775 776 777 778 779 780 781 782 783 784 785 786 787 788 790 791
7 3 2 3 2 8 2 1 1 3 3 1 3 2 5 1
792 793 794 795 796 797 798 799 800 801 802 804 805 806 807 808
2 1 2 2 3 2 1 3 19 2 2 6 4 4 1 2
810 811 812 813 814 815 816 818 819 820 821 822 825 826 827 828
7 1 3 1 2 5 3 1 6 11 3 2 4 1 2 3
829 830 831 833 834 835 836 837 838 839 840 841 842 843 844 845
1 8 2 1 3 5 7 1 3 2 5 4 4 2 1 1
846 849 850 851 852 853 855 856 858 859 860 861 863 864 865 866
2 2 13 4 2 2 1 1 1 2 6 1 1 5 3 1
868 869 870 871 872 873 874 875 877 878 879 880 881 882 883 884
5 2 11 1 2 1 2 3 1 4 1 3 1 2 1 1
885 886 888 889 890 891 893 894 896 897 899 900 901 902 903 904
1 1 3 2 1 1 1 4 1 1 1 7 1 1 1 2
905 906 907 908 909 910 911 912 914 915 916 917 918 920 921 922
1 2 4 2 1 4 2 1 2 4 2 1 1 4 1 3
923 924 925 926 929 930 931 933 935 937 939 940 942 944 945 947
1 1 4 3 1 4 2 1 1 3 3 2 1 1 1 1
948 949 950 951 953 954 955 956 957 958 960 961 962 963 964 966
2 2 4 2 2 4 1 2 4 1 7 3 1 1 1 1
967 969 970 971 972 973 974 975 976 978 979 980 981 982 983 984
1 2 2 2 2 3 2 2 3 2 1 2 2 1 1 1
985 986 987 988 990 991 995 998 1000 1001 1003 1004 1005 1007 1008 1009
1 1 1 3 2 1 1 1 7 4 2 1 3 3 1 1
1010 1011 1012 1013 1014 1015 1017 1018 1019 1020 1021 1022 1023 1027 1028 1030
1 1 1 1 3 1 1 1 2 1 1 2 1 2 1 4
1032 1036 1037 1038 1040 1042 1044 1045 1047 1048 1049 1050 1051 1053 1054 1059
2 1 1 1 1 1 1 1 1 2 1 4 2 1 1 1
1060 1061 1062 1063 1064 1066 1070 1071 1073 1074 1077 1080 1082 1083 1085 1087
2 1 2 1 1 1 3 3 1 1 1 3 1 1 1 4
1088 1090 1093 1095 1098 1100 1106 1108 1110 1113 1118 1121 1123 1124 1127 1131
1 2 1 1 2 4 1 1 2 1 1 1 1 1 2 1
1132 1135 1137 1141 1142 1143 1144 1147 1150 1154 1158 1160 1165 1166 1167 1170
1 1 1 4 1 1 1 1 3 2 1 1 1 1 1 2
1172 1173 1175 1176 1177 1181 1182 1184 1188 1190 1191 1200 1204 1206 1209 1210
2 1 1 2 1 1 1 2 1 3 1 4 1 1 1 7
1211 1213 1217 1218 1220 1224 1225 1229 1234 1236 1240 1246 1250 1251 1256 1257
1 1 1 1 2 1 4 1 1 1 1 1 3 2 1 1
1261 1265 1270 1275 1279 1280 1285 1290 1296 1304 1310 1312 1315 1318 1320 1322
1 1 2 1 1 1 1 1 1 1 3 2 1 1 1 1
1325 1327 1333 1335 1338 1339 1343 1346 1350 1353 1354 1356 1357 1360 1372 1375
1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1377 1385 1395 1398 1399 1400 1416 1420 1421 1427 1428 1432 1433 1441 1448 1453
1 1 2 1 1 1 1 2 1 1 1 1 1 1 1 1
1455 1460 1461 1465 1475 1489 1508 1509 1519 1520 1524 1528 1541 1544 1560 1563
1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1
1568 1572 1606 1614 1620 1624 1637 1644 1664 1684 1699 1725 1760 1816 2035
1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 # non ha senso usare la distribuzione di frequenza perchè non riassume la distribuzione a causa dell'alto numero di modalità diverse (è necessario creare classi di valori)
# la modalità che si presenta più spesso è 5 metri (altitudine di 51 comuni)
# media aritmetica
mean(daticom$alt)[1] 354.6885# l'altitudine media è di circa 355 metri
# mediana
median(daticom$alt)[1] 289# almeno il 50% dei comuni ha un'altitudine <= 289 metri
# almeno il 50% dei comuni ha un'altitudine >= 289 metri
min(daticom$alt)[1] 0max(daticom$alt)[1] 2035Lab 3
Esercizio 1
Si consideri nuovamente il dataframe dati relativo ai dati dei comuni italiani, già considerato per il Lab 3.
dati = read.csv("./data/DatiCom.csv")Caricare la libreria tidyverse.
library(tidyverse)── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.4
✔ forcats 1.0.0 ✔ stringr 1.5.0
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.2 ✔ tidyr 1.3.0
✔ purrr 1.0.2
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors- Creare una nuova variabile denominata
densche rappresenta la densità di popolazione. Essa è data dal rapporto tra la popolazione residente e la superficie del comune.
dati = dati %>%
mutate(dens=pop/sup)
str(dati)'data.frame': 7900 obs. of 12 variables:
$ codreg : int 1 1 1 1 1 1 1 1 1 1 ...
$ codcom : int 1001 1002 1003 1004 1006 1007 1008 1009 1010 1011 ...
$ nomecom : chr "Agli\x8f" "Airasca" "Ala di Stura" "Albiano d'Ivrea" ...
$ sup : num 13.2 15.7 46.3 11.7 17.9 ...
$ pop : int 2558 3681 465 1628 6280 251 16497 2012 479 810 ...
$ zona_alt: int 3 5 1 3 3 1 3 3 1 1 ...
$ alt : int 315 257 1080 230 364 957 314 306 836 782 ...
$ lito : int 0 0 0 0 0 0 0 0 0 0 ...
$ isol : int 0 0 0 0 0 0 0 0 0 0 ...
$ cost : int 0 0 0 0 0 0 0 0 0 0 ...
$ urban : int 2 3 3 3 2 3 2 3 3 3 ...
$ dens : num 195 234 10 139 351 ...- Creare una nuova variabile
urban2andando a ricodificare la variabileurbansecondo le seguenti categorie: 1=Zone densamente popolate; 2=Zone a densità intermedia; 3=Zone scarsamente popolate.
dati = dati %>%
mutate(urban2 = case_when(
urban == 1 ~ "Zone densamente popolate",
urban == 2 ~ "Zone a densità intermedia",
urban == 3 ~ "Zone scarsamente popolate"
))
str(dati)'data.frame': 7900 obs. of 13 variables:
$ codreg : int 1 1 1 1 1 1 1 1 1 1 ...
$ codcom : int 1001 1002 1003 1004 1006 1007 1008 1009 1010 1011 ...
$ nomecom : chr "Agli\x8f" "Airasca" "Ala di Stura" "Albiano d'Ivrea" ...
$ sup : num 13.2 15.7 46.3 11.7 17.9 ...
$ pop : int 2558 3681 465 1628 6280 251 16497 2012 479 810 ...
$ zona_alt: int 3 5 1 3 3 1 3 3 1 1 ...
$ alt : int 315 257 1080 230 364 957 314 306 836 782 ...
$ lito : int 0 0 0 0 0 0 0 0 0 0 ...
$ isol : int 0 0 0 0 0 0 0 0 0 0 ...
$ cost : int 0 0 0 0 0 0 0 0 0 0 ...
$ urban : int 2 3 3 3 2 3 2 3 3 3 ...
$ dens : num 195 234 10 139 351 ...
$ urban2 : chr "Zone a densità intermedia" "Zone scarsamente popolate" "Zone scarsamente popolate" "Zone scarsamente popolate" ...- Ricavare la distribuzione di frequenza della variabile
urban2usando anche le frequenze percentuali. Quale è la moda della distribuzione?
dati %>%
count(urban2) %>%
mutate(perc =round(n/sum(n)*100,2)) urban2 n perc
1 Zone a densità intermedia 2606 32.99
2 Zone densamente popolate 255 3.23
3 Zone scarsamente popolate 5039 63.78# La moda è Zone scarsamente popolate- Calcolare la densità di popolazione media dei comuni italiani usando
dens. Commentare.
dati %>%
summarise(mean(dens)) mean(dens)
1 298.1274# in media la densità è 298 abitanti per kmq- Calcolare la densità di popolazione media dei comuni italiani usando
dens, condizionatamente alle categorie diurban2. Commentare.
dati %>%
group_by(urban2) %>%
summarise(mean(dens))# A tibble: 3 × 2
urban2 `mean(dens)`
<chr> <dbl>
1 Zone a densità intermedia 512.
2 Zone densamente popolate 2406.
3 Zone scarsamente popolate 81.0# come ci si aspetta la densità media di pop.
# è maggiore per le zone densamente popolate- Creare un nuovo dataframe
smalldatiche contiene solamente le colonnecodcom,supepop.
smalldati = dati %>%
select(codcom, sup, pop)
str(smalldati)'data.frame': 7900 obs. of 3 variables:
$ codcom: int 1001 1002 1003 1004 1006 1007 1008 1009 1010 1011 ...
$ sup : num 13.2 15.7 46.3 11.7 17.9 ...
$ pop : int 2558 3681 465 1628 6280 251 16497 2012 479 810 ...head(smalldati) #prime 6 righe codcom sup pop
1 1001 13.15 2558
2 1002 15.74 3681
3 1003 46.33 465
4 1004 11.73 1628
5 1006 17.88 6280
6 1007 5.63 251Lab 4
Esercizio 1
Si consideri nuovamente il dataframe dati relativo ai dati dei comuni italiani, già considerato per il Lab 3 e 4:
dati = read.csv("./data/DatiCom.csv")Caricare la libreria tidyverse.
library(tidyverse)- Creare la variabile
urban2come ricodificare della variabileurbanusando le categorie 1=“densamente pop”, 2=“mediamente pop”, 3=“scarsamente pop”. Costruire la distribuzione di frequenza diurban2. Quale è la moda diurban2?
dati = dati %>%
mutate(urban2 = case_when(
urban == 1 ~ "densamente pop",
urban == 2 ~ "mediamente pop",
urban == 3 ~ "scarsamente pop"
))
dati %>%
count(urban2) urban2 n
1 densamente pop 255
2 mediamente pop 2606
3 scarsamente pop 5039# la maggior parte dei comuni italiani è scarsamente popolato (moda)- Rappresentare graficamente la variabile
urban2. Usare il colore marrone per il bordo e l’arancio per il riempimento.
dati %>%
ggplot()+
geom_bar(aes(urban2), col="brown", fill="orange")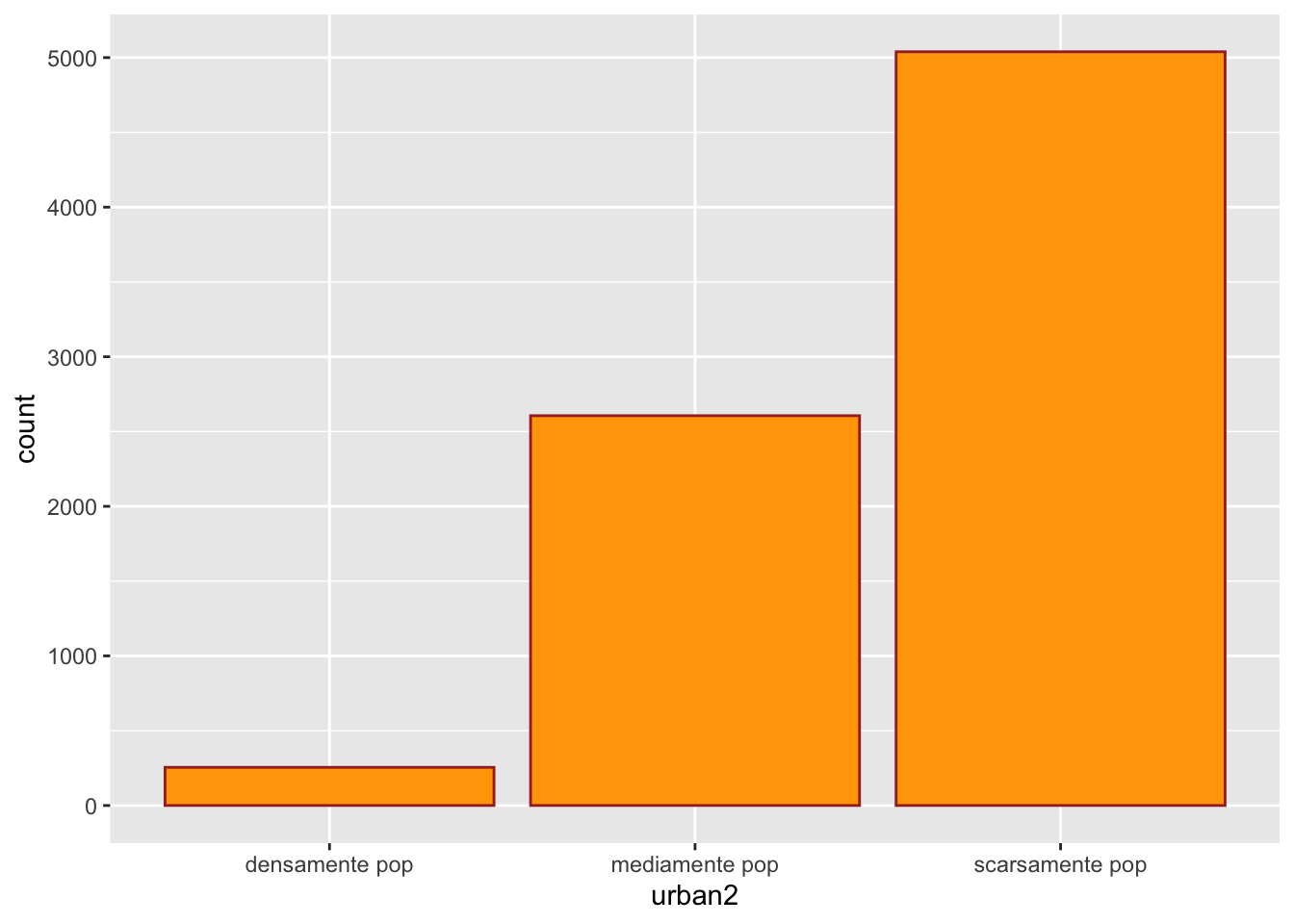
- Selezionare solo i comuni nella regione Piemonte (
codreguguale a 1) creando un nuovo dataframe denominatodatipiem. Quanti comuni ci sono in Piemonte?
datipiem = dati %>%
filter(codreg == 1)
nrow(datipiem) #n. di comuni[1] 1180- Quanti comuni densamente popolati ci sono in Piemonte? Quali sono?
datipiem %>%
count(urban2) urban2 n
1 densamente pop 4
2 mediamente pop 232
3 scarsamente pop 944# solo 4 densamente popolati
datipiem %>%
filter(urban2 == "densamente pop") codreg codcom nomecom sup pop zona_alt alt lito isol cost urban
1 1 1272 Torino 130.06 841600 5 239 0 0 0 1
2 1 3106 Novara 103.05 101257 5 162 0 0 0 1
3 1 5005 Asti 151.31 73421 3 123 0 0 0 1
4 1 6003 Alessandria 203.57 91059 5 95 0 0 0 1
urban2
1 densamente pop
2 densamente pop
3 densamente pop
4 densamente pop# capoluoghi di provincia- Considerando i dati piemontesi, si voglia ora studiare l’altitudine sul livello del mare (
alt). Quale è l’altitudine maggiore? A quale comune corrisponde? E quella minore? E quella media?
datipiem %>%
filter(alt == max(alt)) #2035 metri - Sestriere codreg codcom nomecom sup pop zona_alt alt lito isol cost urban
1 1 1263 Sestriere 25.92 929 1 2035 0 0 0 3
urban2
1 scarsamente popdatipiem %>%
filter(alt == max(alt)) #2 comuni a 76 metri codreg codcom nomecom sup pop zona_alt alt lito isol cost urban
1 1 1263 Sestriere 25.92 929 1 2035 0 0 0 3
urban2
1 scarsamente popmean(datipiem$alt) #altitudine media dei comuni piemontesi[1] 416.7119- Rappresentare graficamente l’altitudine dei comuni piemontesi usando l’istogramma. La distribuzione è simmetrica?
datipiem %>%
ggplot() +
geom_histogram(aes(alt), col="orange")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.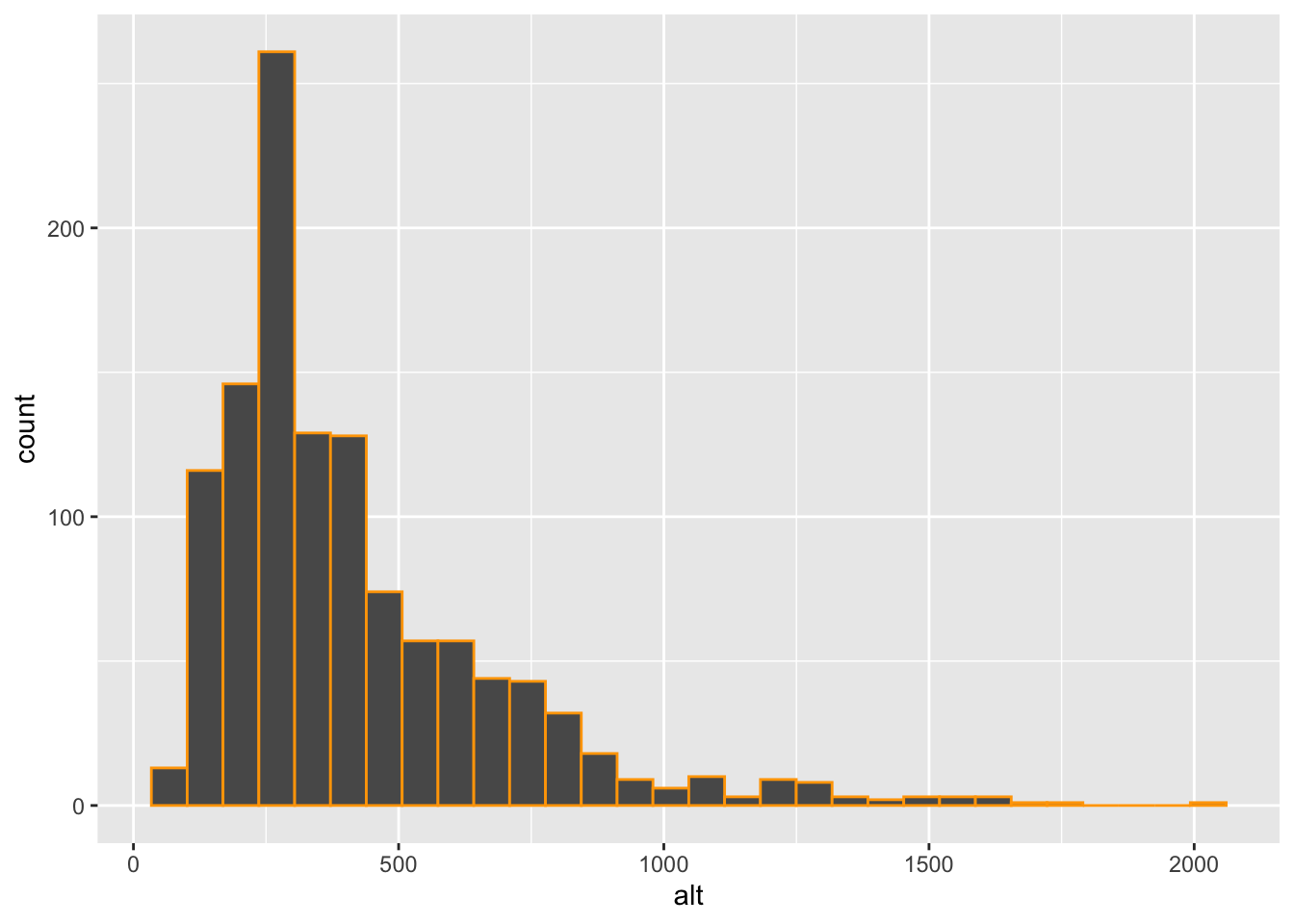
# No, la maggior parte dei comuni è collocata a sinistra, coda lunga a destra (pochi comuni con altitudine elevata) - Modificare l’istogramma in modo da avere sottografici a seconda delle categorie di
urban2.
datipiem %>%
ggplot() +
geom_histogram(aes(alt, fill=urban2), col="orange")+
facet_wrap(~urban2) +
xlab("Altitudine sul livello del mare (in metri, in classi)") +
ylab("Frequenze assolute")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.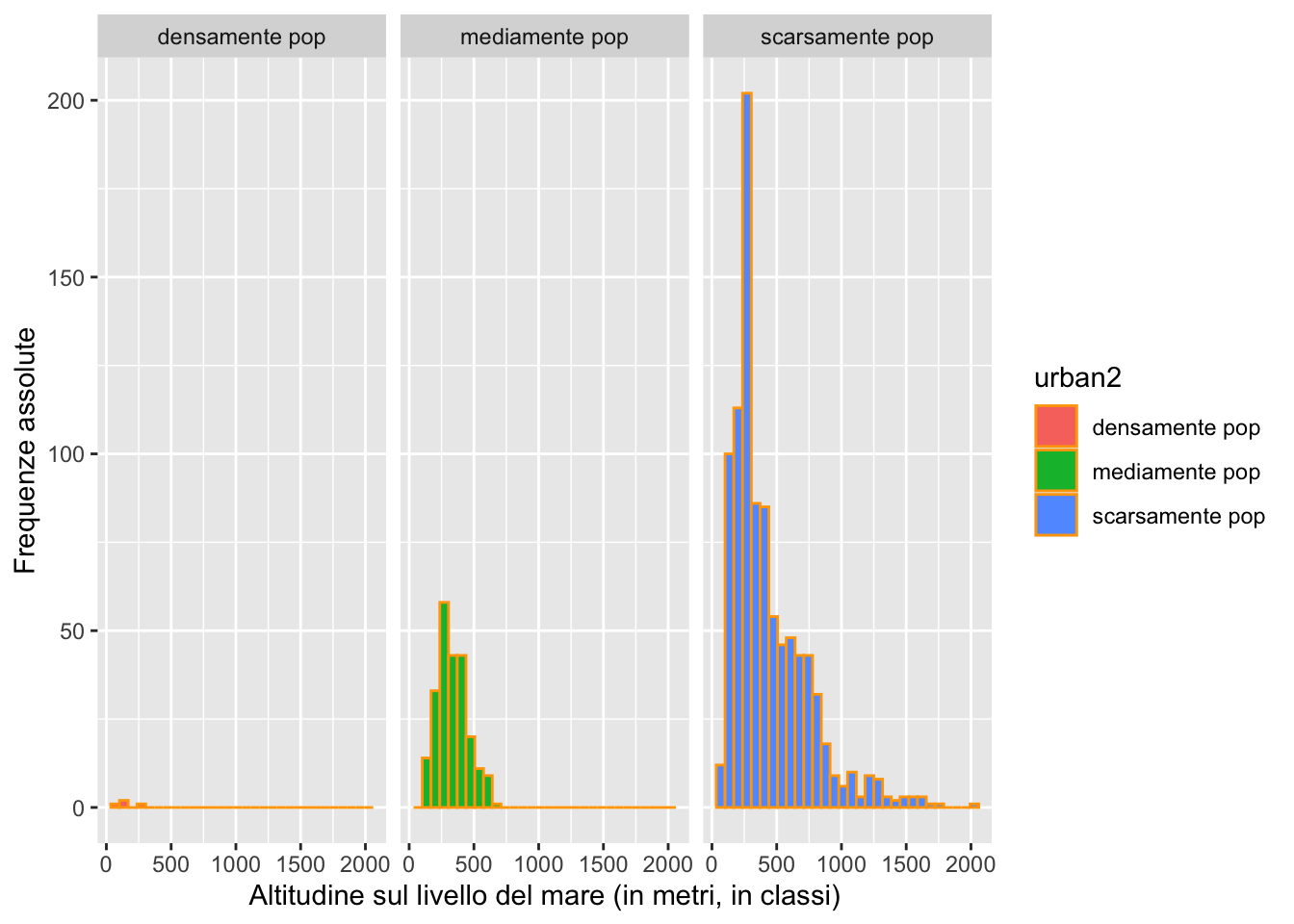
# la distribuzione di sinistra si riferisce ai 4 capoluoghi di provincia (densamente popolati) che si trovano a basse altitudini
# i comuni scarsamente popolati sono quelli con la numerosità più elevata e con la maggiore variabilità in termini di altitudine- Calcolare l’altitudine minima, media, massima, la varianza e il coefficiente di variazione condizionatamente a
urban2. Commentare.
datipiem %>%
group_by(urban2) %>%
summarise(min(alt), max(alt), mean(alt), var(alt), sd(alt)/mean(alt))# A tibble: 3 × 6
urban2 `min(alt)` `max(alt)` `mean(alt)` `var(alt)` `sd(alt)/mean(alt)`
<chr> <int> <int> <dbl> <dbl> <dbl>
1 densamente p… 95 239 155. 3910. 0.404
2 mediamente p… 116 646 336. 14012. 0.353
3 scarsamente … 76 2035 438. 87896. 0.677# I comuni scarsamente popolati sono mediamente collocati ad una quota maggiore (438 metri)
# I comuni scarsamente popolati sono quelli con maggiore variabilità (CV = 0.677)Lab 5
Esercizio 1
Si considerino i dati contenuti nel file agriturismi.csv che riportano il numero di agriturismi per fascia altimetrica (montagna, collina, pianura) per l’anno 2022 (fonte: Istat).
- Importare i dati in
RStudiocreando un oggetto di nomeagr. Quali sono le sue dimensioni?
agr = read.csv("./data/agriturismi.csv")
dim(agr) #20 regioni x 4 colonne[1] 20 4glimpse(agr)Rows: 20
Columns: 4
$ Regione <chr> "Piemonte", "Valle d'Aosta-Vallèe Aoste", "Lombardia", "Ligur…
$ Montagna <int> 261, 60, 506, 268, 3907, 289, 99, 204, 718, 217, 227, 161, 20…
$ Collina <int> 952, 0, 560, 477, 0, 598, 253, 573, 4499, 1079, 903, 880, 380…
$ Pianura <int> 200, 0, 672, 0, 0, 726, 359, 446, 417, 0, 0, 263, 0, 0, 85, 5…- Fare il reshape dei dati da formato wide a formato long creando un nuovo dataframe denominato
agrlongcon 3 colonne (Regione,fascia_alten_agr). Quali sono le dimensioni diagrlong?
agrlong = agr %>%
pivot_longer(Montagna:Pianura,
names_to = "fascia_alt",
values_to = "n_agr")
dim(agrlong)[1] 60 3glimpse(agrlong) Rows: 60
Columns: 3
$ Regione <chr> "Piemonte", "Piemonte", "Piemonte", "Valle d'Aosta-Vallèe A…
$ fascia_alt <chr> "Montagna", "Collina", "Pianura", "Montagna", "Collina", "P…
$ n_agr <int> 261, 952, 200, 60, 0, 0, 506, 560, 672, 268, 477, 0, 3907, …- Calcolare il numero totale di agriturismi per ogni regione (considerando insieme tutte le fasce altimetriche). Quale regione ha il maggior numero totale di agriturismi?
agrlong %>%
group_by(Regione) %>%
summarise(sum(n_agr))# A tibble: 20 × 2
Regione `sum(n_agr)`
<chr> <int>
1 Abruzzo 586
2 Basilicata 211
3 Calabria 553
4 Campania 897
5 Emilia-Romagna 1223
6 Friuli-Venezia Giulia 711
7 Lazio 1304
8 Liguria 745
9 Lombardia 1738
10 Marche 1130
11 Molise 116
12 Piemonte 1413
13 Puglia 960
14 Sardegna 777
15 Sicilia 975
16 Toscana 5634
17 Trentino-Alto Adige/Sudtirol 3907
18 Umbria 1296
19 Valle d'Aosta-Vallèe Aoste 60
20 Veneto 1613# Toscana 5634 agriturismi - Calcolare il numero totale di agriturismi per fascia altimetrica (considerando insieme tutte le regioni). Quale fascia altimetrica ha il maggior numero totale di agriturismi?
agrlong %>%
group_by(fascia_alt) %>%
summarise(sum(n_agr))# A tibble: 3 × 2
fascia_alt `sum(n_agr)`
<chr> <int>
1 Collina 13788
2 Montagna 7963
3 Pianura 4098# collina 689 agriturismi - Si consideri la regione Trentino. Calcolare il numero totale di agriturismi condiziontamente alla fascia altimetrica. Commentare.
agrlong %>%
filter(Regione == "Trentino-Alto Adige/Sudtirol") %>%
group_by(fascia_alt) %>%
summarise(sum(n_agr))# A tibble: 3 × 2
fascia_alt `sum(n_agr)`
<chr> <int>
1 Collina 0
2 Montagna 3907
3 Pianura 0# tutti gli agriturismi sono in montagna- Utilizzare dei boxplot per rappresentare la distribuzione del numero di agriturismi per fascia altimetrica. Commentare. Calcolare inoltre i quartili con cui sono stati costruite le 3 scatole.
agrlong %>%
ggplot() +
geom_boxplot(aes(fascia_alt, n_agr))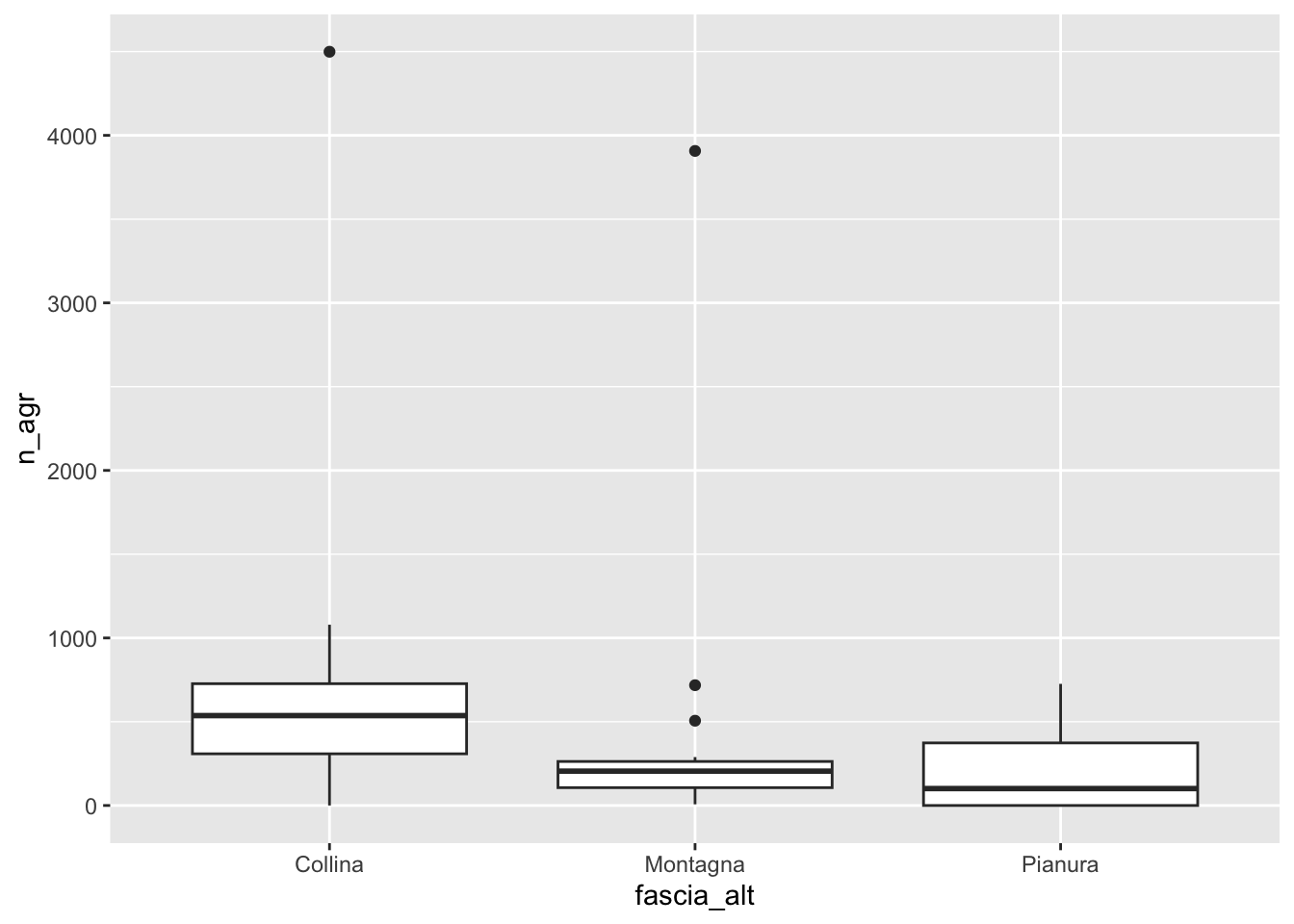 
# mediana più alta per collina
# minore variabilità per montagna
# valori estremi per collina e montagna
agrlong %>%
group_by(fascia_alt) %>%
summarise(Q1 = quantile(n_agr, 0.25),
Q2 = median(n_agr),
Q3 = quantile(n_agr, 0.75)) %>%
mutate(IQR = Q3-Q1)# A tibble: 3 × 5
fascia_alt Q1 Q2 Q3 IQR
<chr> <dbl> <dbl> <dbl> <dbl>
1 Collina 308. 536. 727 418.
2 Montagna 106. 205 263. 156.
3 Pianura 0 101 374. 374.- Considerando la fascia altimetrica collinare, quale regione risulta essere un outlier?
agrlong %>%
filter(fascia_alt == "Collina", n_agr > 4000) # A tibble: 1 × 3
Regione fascia_alt n_agr
<chr> <chr> <int>
1 Toscana Collina 4499- Considerando la fascia altimetrica di montagna, quali regioni risultano più agriturismi?
agrlong %>%
filter(fascia_alt == "Montagna") %>%
top_n(3, n_agr)# A tibble: 3 × 3
Regione fascia_alt n_agr
<chr> <chr> <int>
1 Lombardia Montagna 506
2 Trentino-Alto Adige/Sudtirol Montagna 3907
3 Toscana Montagna 718Lab 6
Esercizio 1
Continuare ad utilizzare l’oggetto biblio creato nel Laboratorio 6.
- Ricavare la distribuzione di frequenza e rappresentare graficamente la distribuzione della variabile
tipocondizionatamente alla variabileprovincia. In quale provincia si osserva la maggiore/minore presenza di biblioteche private?
biblio %>%
ggplot() +
geom_bar(aes(provincia, fill=tipo),
position="fill") +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1, size=4)) # per ruotare il testo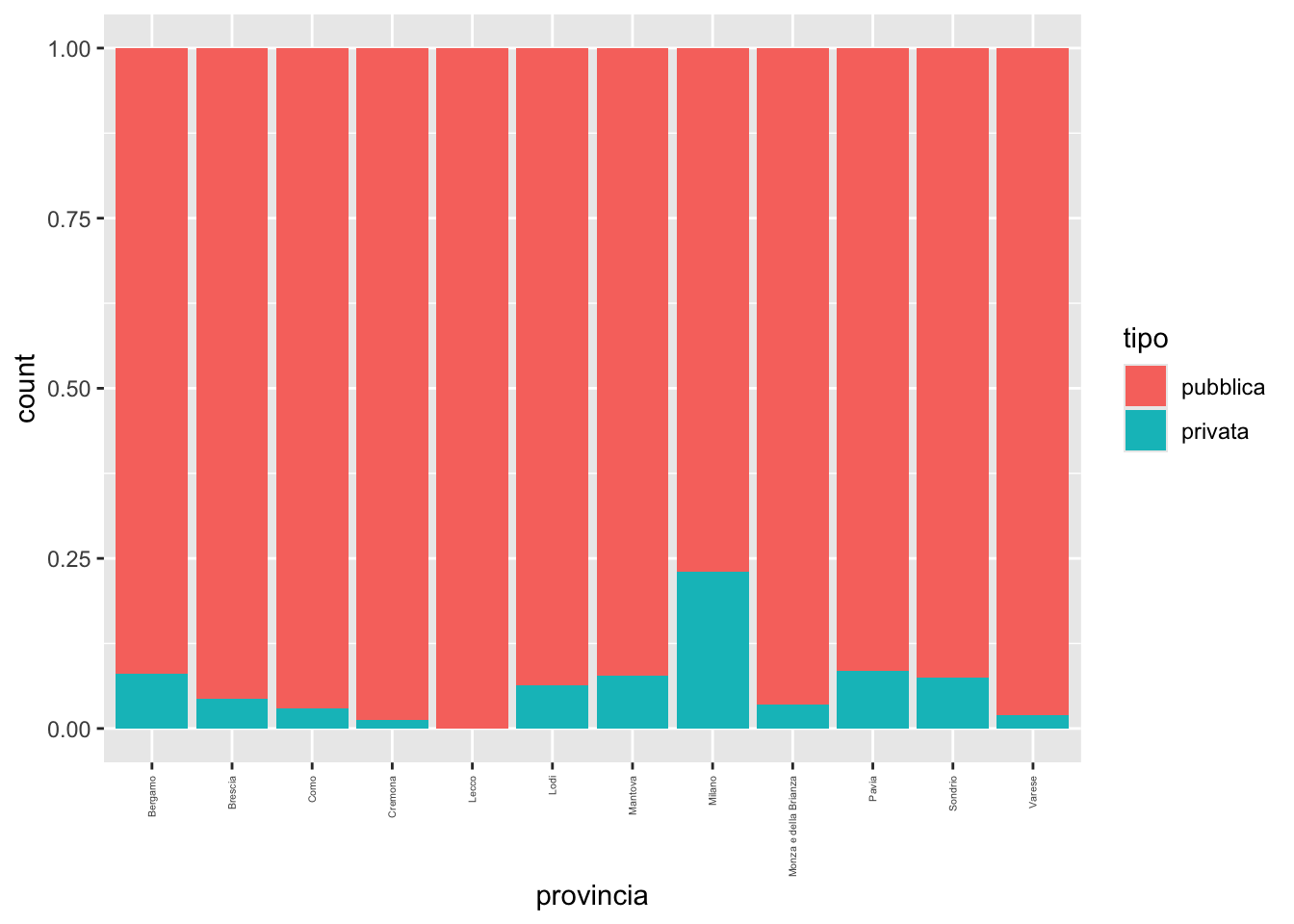
biblio %>%
group_by(provincia) %>%
count(provincia, tipo) %>%
mutate(perc=n/sum(n)*100) %>%
print(n=100)# A tibble: 23 × 4
# Groups: provincia [12]
provincia tipo n perc
<chr> <fct> <int> <dbl>
1 Bergamo pubblica 204 91.9
2 Bergamo privata 18 8.11
3 Brescia pubblica 197 95.6
4 Brescia privata 9 4.37
5 Como pubblica 97 97
6 Como privata 3 3
7 Cremona pubblica 76 98.7
8 Cremona privata 1 1.30
9 Lecco pubblica 59 100
10 Lodi pubblica 44 93.6
11 Lodi privata 3 6.38
12 Mantova pubblica 71 92.2
13 Mantova privata 6 7.79
14 Milano pubblica 170 76.9
15 Milano privata 51 23.1
16 Monza e della Brianza pubblica 56 96.6
17 Monza e della Brianza privata 2 3.45
18 Pavia pubblica 76 91.6
19 Pavia privata 7 8.43
20 Sondrio pubblica 37 92.5
21 Sondrio privata 3 7.5
22 Varese pubblica 102 98.1
23 Varese privata 2 1.92# la maggiore a Milano: il 23.1% dell biblioteche milanese è privata
# la minore a Lecco dove non sono presenti biblioteche private- Rappresentare graficamente i caratteri
nutentienlibri. Colorare i puntini in funzione dellaprovincia. Dopo aver calcolato la correlazione tra le due variabili commentare.
biblio %>%
ggplot() +
geom_point(aes(nutenti, nlibri, col=provincia))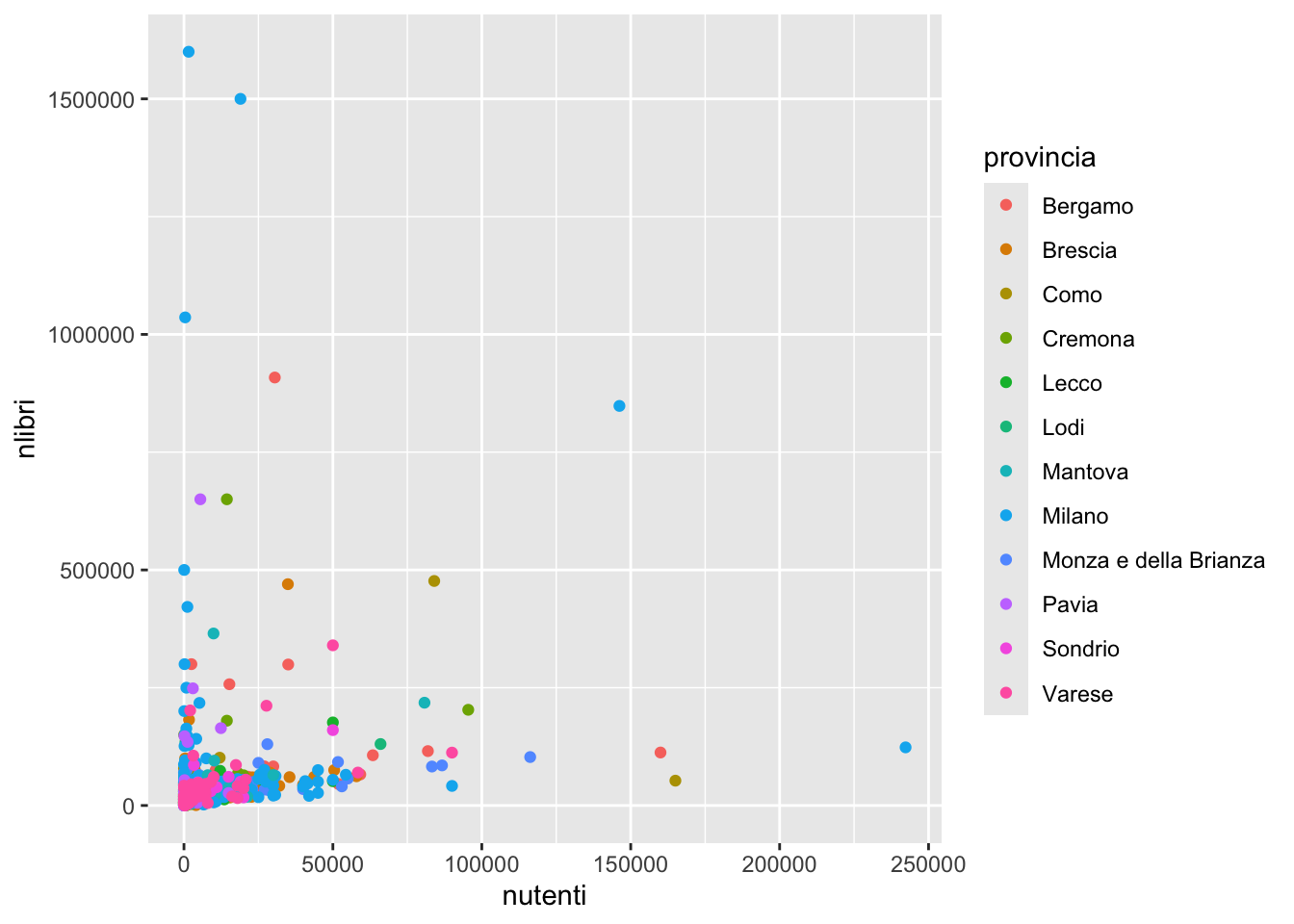
cor(biblio$nlibri,biblio$nutenti)[1] 0.2586133# correlazione positiva e bassa
# in effetti la nuvola dei punti non tende a disporsi lungo una retta- Trovare a quale biblioteca si riferiscono i 3 pallini in alto a sinistra nel grafico.
biblio %>%
filter(nlibri>1000000) provincia comune
1 Milano Milano
2 Milano Milano
3 Milano Milano
denominaz
1 Biblioteca Ambrosiana
2 Biblioteca nazionale Braidense
3 Biblioteca e Archivio - Civica Raccolta delle Stampe Achille Bertarelli
tipo nposti npc wifi nutenti nlibri nlibrinew22
1 privata 25 1 sì 1577 1600000 50000
2 pubblica 100 2 sì 18979 1500000 22000
3 pubblica 16 2 sì 405 1036095 100- Rappresentare graficamente la distribuzione della variabile
nutentiin funzione dellaprovincia. Commentare.
biblio %>%
ggplot() +
geom_boxplot(aes(provincia, nutenti)) +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1, size=4))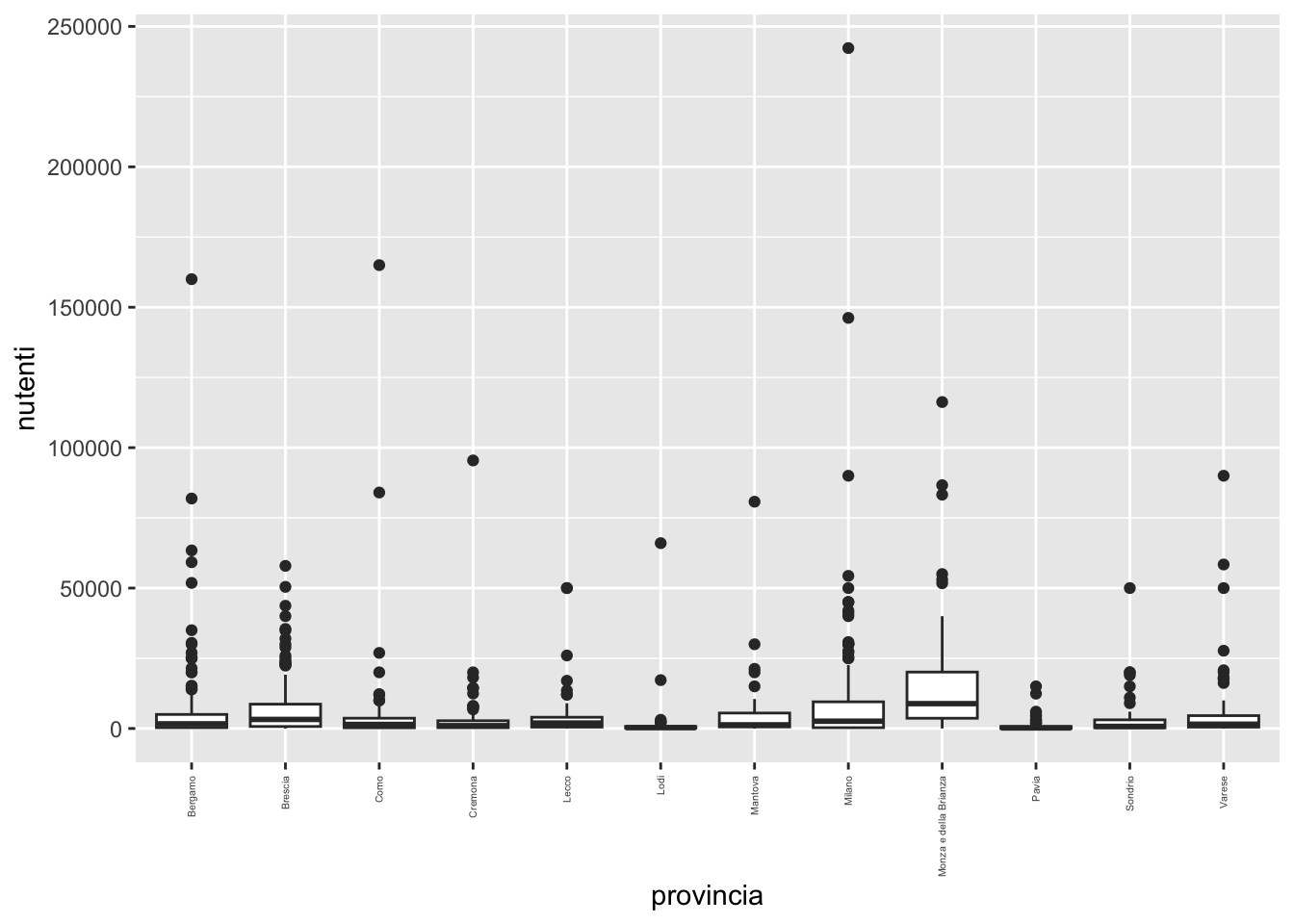 
# tutti i boxplot presentano valori estremi (biblioteche con numero di utenti estremo)
# Brescia, Milano, e MB sembrano avere un valore mediano del numero di utenti maggiore- Calcolare per ogni provincia il numero medio e mediano del numero di utenti insieme al coefficiente di variazione.
biblio %>%
group_by(provincia) %>%
summarise(media = mean(nutenti),
mediana = median(nutenti),
cv = sd(nutenti)/mean(nutenti))# A tibble: 12 × 4
provincia media mediana cv
<chr> <dbl> <dbl> <dbl>
1 Bergamo 5698. 1656. 2.54
2 Brescia 6803. 3225 1.38
3 Como 5130. 1450 3.61
4 Cremona 3805. 1000 2.98
5 Lecco 4892. 1940 1.99
6 Lodi 2304. 300 4.26
7 Mantova 4639. 1300 2.21
8 Milano 9309. 2600 2.36
9 Monza e della Brianza 16698. 8850 1.37
10 Pavia 1059. 200 2.25
11 Sondrio 4482. 750 2.08
12 Varese 5182. 1525 2.33# i valori di mediana confermano quanto visto nei boxplot
# la maggiore variabilità (CV) si osserva a Lodi- Rappresentare graficamente la distribuzione del carattere
nlibrinew22(nuovi libri acquistati nel 2022). Calcolare inoltre e commentare i quartili. Infine, identificare la biblioteca che nel 2022 ha comprato il maggior numero di libri.
biblio %>%
ggplot() +
geom_histogram(aes(nlibrinew22),
col="lightgreen")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.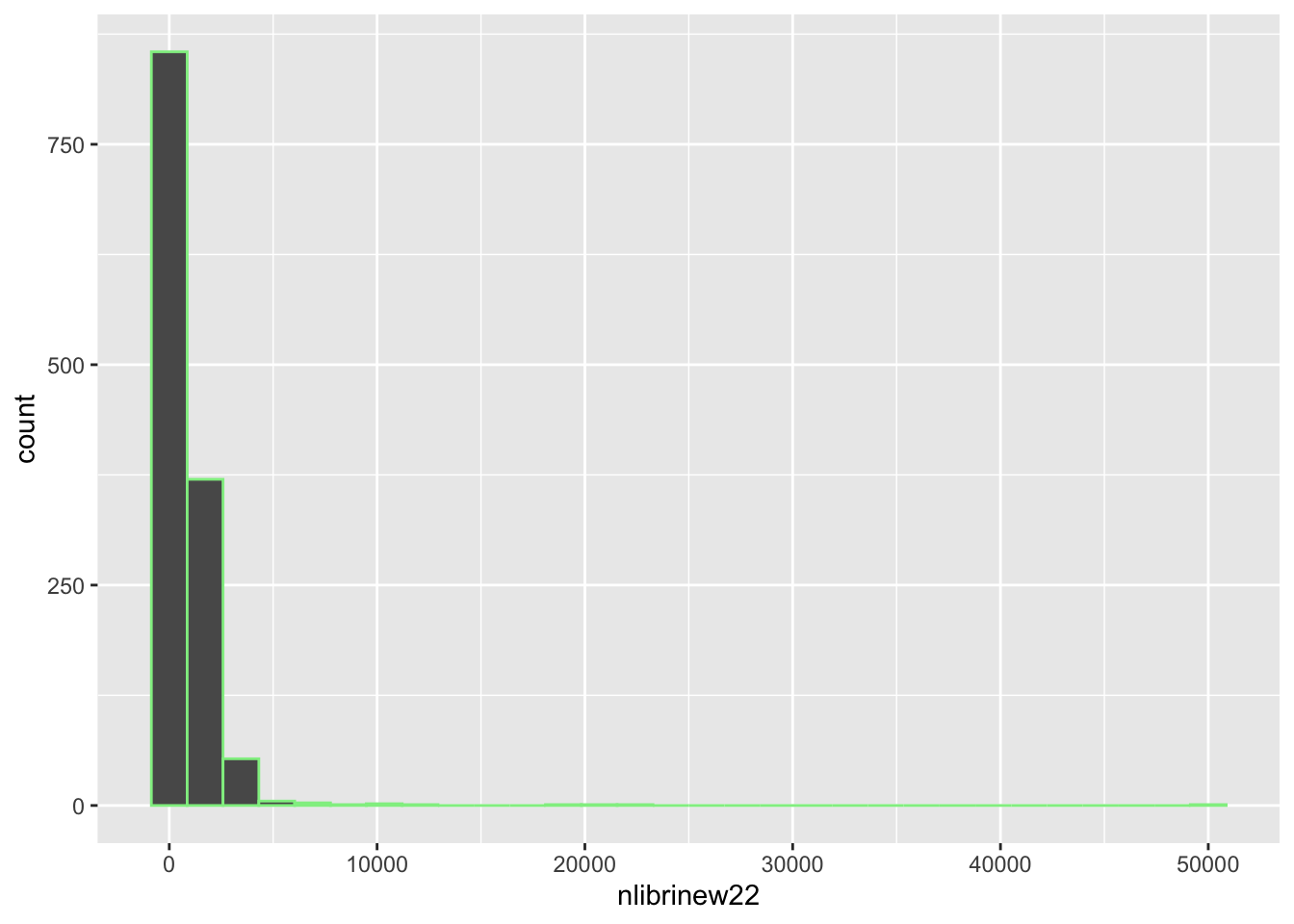
biblio %>%
summarise(Q1=quantile(nlibrinew22,0.25),
Q2=median(nlibrinew22),
Q3=quantile(nlibrinew22, 0.75)) Q1 Q2 Q3
1 285.75 550 1149.75# il 25% circa delle biblioteche ha comprato nel 2022 un n. di libri <= 285.75
# il 50% circa delle biblioteche ha comprato nel 2022 un n. di libri <= 550
# il 75% circa delle biblioteche ha comprato nel 2022 un n. di libri <= 1149.75
biblio %>%
filter(nlibrinew22==max(nlibrinew22)) provincia comune
1 Milano Milano
denominaz
1 Biblioteca Ambrosiana
tipo nposti npc wifi nutenti nlibri nlibrinew22
1 privata 25 1 sì 1577 1600000 50000# 50000 nuovi libri per la biblioteca ambrosiana- Utilizzando
nlibrienlibrinew22calcolare per ogni biblioteca quanti libri erano presenti nel 2021 (creare una nuova variabilenlibri21).
biblio = biblio %>%
mutate(nlibri21 = nlibri - nlibrinew22)
glimpse(biblio)Rows: 1,294
Columns: 11
$ provincia <chr> "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Be…
$ comune <fct> Adrara San Martino , Adrara…
$ denominaz <fct> "Biblioteca comunale …
$ tipo <fct> pubblica, pubblica, pubblica, pubblica, pubblica, pubblica…
$ nposti <int> 30, 34, 46, 150, 20, 35, 30, 24, 15, 50, 18, 22, 5, 20, 41…
$ npc <int> 2, 1, 3, 2, 1, 0, 8, 2, 3, 4, 2, 3, 0, 0, 3, 0, 3, 0, 2, 0…
$ wifi <fct> sì, no, sì, sì, sì, sì, sì, sì, sì, sì, sì, sì, no, sì, sì…
$ nutenti <int> 1000, 52, 2589, 63416, 5600, 12000, 7000, 0, 530, 3000, 39…
$ nlibri <int> 6492, 7093, 35432, 106640, 33163, 33614, 19162, 17875, 116…
$ nlibrinew22 <int> 339, 449, 1642, 2153, 1452, 2004, 644, 393, 719, 912, 863,…
$ nlibri21 <int> 6153, 6644, 33790, 104487, 31711, 31610, 18518, 17482, 109…- Calcolare quante biblioteche non hanno acquistato libri nuovi nel 2022 ed eliminarle (creare
biblio2).
biblio %>%
summarise(sum(nlibrinew22 == 0)) sum(nlibrinew22 == 0)
1 59# 59 biblioteche
biblio2 = biblio %>%
filter(nlibrinew22 > 0)- Usando
biblio2calcolare una nuova variabile (Delta) che calcoli l’incremento percentuale nel numero di libri dal 2021 al 2022 usando la seguente formula: \[ \Delta = \frac{y_{2022}-y_{2021}}{y_{2022}}\cdot 100 \]
biblio2 = biblio2 %>%
mutate(Delta = (nlibri-nlibri21)/nlibri21 * 100)
glimpse(biblio2)Rows: 1,235
Columns: 12
$ provincia <chr> "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Be…
$ comune <fct> Adrara San Martino , Adrara…
$ denominaz <fct> "Biblioteca comunale …
$ tipo <fct> pubblica, pubblica, pubblica, pubblica, pubblica, pubblica…
$ nposti <int> 30, 34, 46, 150, 20, 35, 30, 24, 15, 50, 18, 22, 5, 20, 41…
$ npc <int> 2, 1, 3, 2, 1, 0, 8, 2, 3, 4, 2, 3, 0, 0, 3, 0, 3, 0, 2, 2…
$ wifi <fct> sì, no, sì, sì, sì, sì, sì, sì, sì, sì, sì, sì, no, sì, sì…
$ nutenti <int> 1000, 52, 2589, 63416, 5600, 12000, 7000, 0, 530, 3000, 39…
$ nlibri <int> 6492, 7093, 35432, 106640, 33163, 33614, 19162, 17875, 116…
$ nlibrinew22 <int> 339, 449, 1642, 2153, 1452, 2004, 644, 393, 719, 912, 863,…
$ nlibri21 <int> 6153, 6644, 33790, 104487, 31711, 31610, 18518, 17482, 109…
$ Delta <dbl> 5.5095076, 6.7579771, 4.8594259, 2.0605434, 4.5788528, 6.3…biblio2 %>%
filter(Delta < 0) provincia comune
1 Bergamo Ponte San Pietro
denominaz
1 Biblioteca del Sistema bibliotecario dell�area Nord-Ovest della provincia di Bergamo
tipo nposti npc wifi nutenti nlibri nlibrinew22 nlibri21 Delta
1 pubblica 4 0 no 12 0 96 -96 -100- Ricavare il valore minimo e massimo di
Deltae capire a quale biblioteche corrispondono. Se i valori sono anomali eliminare le biblioteche.
biblio2 %>%
summarise(min(Delta), max(Delta)) min(Delta) max(Delta)
1 -100 Infbiblio2 %>% filter(Delta<0) provincia comune
1 Bergamo Ponte San Pietro
denominaz
1 Biblioteca del Sistema bibliotecario dell�area Nord-Ovest della provincia di Bergamo
tipo nposti npc wifi nutenti nlibri nlibrinew22 nlibri21 Delta
1 pubblica 4 0 no 12 0 96 -96 -100# forse questo è un errore nel dataframe perchè per questa biblioteca risultano 0 libri nel 2022 e 96 libri comprati nel 2022
biblio2 %>% filter(Delta == max(Delta)) provincia comune
1 Bergamo Luzzana
2 Lodi Villanova del Sillaro
denominaz
1 biblioteca comunale
2 Biblioteca Abbaziale di Villanova del Sillaro
tipo nposti npc wifi nutenti nlibri nlibrinew22 nlibri21 Delta
1 pubblica 16 2 sì 600 207 207 0 Inf
2 pubblica 6 0 no 100 550 550 0 Inf# due biblioteche che avevano 0 libri nel 21 e ne hanno comprati 207 e 550 nel 22- Dopo aver eliminato i valori anomali di cui sopra, calcolare il valore di
Deltamedio.
biblio2 %>%
filter(Delta>0, Delta < "Inf") %>%
summarise(mean(Delta)) mean(Delta)
1 5.998239# in media il patrimonio delle biblioteche dal 2021 al 2022 è aumentato del 5.99%Lab 7
Esercizio 1
Si considerino i dati contenuti nel file pilprocapite.csv relativi al pil procapite (in migliaia di euro) per le regioni italiane per gli anni 2020-2022 (fonte: Istat).
- Importare i dati in R creando un oggetto di nome pil. Esplorare il data frame.
library(tidyverse)
pil = read.csv("./data/pilprocapite.csv",
stringsAsFactors = T)
glimpse(pil)Rows: 20
Columns: 5
$ codreg <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …
$ TERRITORIO <fct> Piemonte, Valle d'Aosta / Vallée d'Aoste, Lombardia, Trenti…
$ X2020 <dbl> 29.6, 35.8, 37.5, 41.0, 31.3, 30.4, 29.8, 34.2, 29.2, 24.3,…
$ X2021 <dbl> 32.6, 38.6, 41.8, 44.4, 34.6, 33.8, 32.7, 38.0, 32.3, 26.7,…
$ X2022 <dbl> 34.4, 43.7, 44.4, 49.4, 37.2, 36.0, 35.8, 40.0, 35.1, 28.2,…- Fare il join di
pilcon lo shapefile (oggesttosf) delle regioni italiane usato nel Laboratorio 7. Creare un nuovo oggetto di tiposfdi nomereg2.
library(sf)Linking to GEOS 3.11.0, GDAL 3.5.3, PROJ 9.1.0; sf_use_s2() is TRUEreg = st_read("./data/Reg01012023_g_WGS84.shp")Reading layer `Reg01012023_g_WGS84' from data source
`/Users/michelacameletti/Library/CloudStorage/GoogleDrive-michela.cameletti@unibg.it/My Drive/UniBg/Didattica/Lingue_GeoUrb/2023-2024/MAD2324Rlabs/data/Reg01012023_g_WGS84.shp'
using driver `ESRI Shapefile'
Simple feature collection with 20 features and 5 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 313279.3 ymin: 3933846 xmax: 1312016 ymax: 5220292
Projected CRS: WGS 84 / UTM zone 32Nreg2 = reg %>%
inner_join(pil,
by = join_by(COD_REG == codreg))
glimpse(reg2)Rows: 20
Columns: 10
$ COD_RIP <dbl> 1, 1, 1, 2, 2, 2, 1, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5
$ COD_REG <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …
$ DEN_REG <chr> "Piemonte", "Valle d'Aosta", "Lombardia", "Trentino-Alto Ad…
$ Shape_Leng <dbl> 1236799.8, 310968.1, 1410222.9, 800893.7, 1054587.0, 670820…
$ Shape_Area <dbl> 25393881930, 3258837561, 23862315752, 13607548167, 18343552…
$ TERRITORIO <fct> Piemonte, Valle d'Aosta / Vallée d'Aoste, Lombardia, Trenti…
$ X2020 <dbl> 29.6, 35.8, 37.5, 41.0, 31.3, 30.4, 29.8, 34.2, 29.2, 24.3,…
$ X2021 <dbl> 32.6, 38.6, 41.8, 44.4, 34.6, 33.8, 32.7, 38.0, 32.3, 26.7,…
$ X2022 <dbl> 34.4, 43.7, 44.4, 49.4, 37.2, 36.0, 35.8, 40.0, 35.1, 28.2,…
$ geometry <MULTIPOLYGON [m]> MULTIPOLYGON (((457749.5 51..., MULTIPOLYGON (((390652.6 50…- Trasformare
reg2da formato wide a formato long ed eliminare eventuali caratteri non necessari.
reg2long = reg2 %>%
pivot_longer(X2020:X2022,
names_to = "anno",
values_to = "pilprocapite")
reg2long = reg2long %>%
mutate(anno = str_replace(anno,"X",""))
glimpse(reg2long)Rows: 60
Columns: 9
$ COD_RIP <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, …
$ COD_REG <dbl> 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, …
$ DEN_REG <chr> "Piemonte", "Piemonte", "Piemonte", "Valle d'Aosta", "Val…
$ Shape_Leng <dbl> 1236799.8, 1236799.8, 1236799.8, 310968.1, 310968.1, 3109…
$ Shape_Area <dbl> 25393881930, 25393881930, 25393881930, 3258837561, 325883…
$ TERRITORIO <fct> Piemonte, Piemonte, Piemonte, Valle d'Aosta / Vallée d'Ao…
$ geometry <MULTIPOLYGON [m]> MULTIPOLYGON (((457749.5 51..., MULTIPOLYGON…
$ anno <chr> "2020", "2021", "2022", "2020", "2021", "2022", "2020", "…
$ pilprocapite <dbl> 29.6, 32.6, 34.4, 35.8, 38.6, 43.7, 37.5, 41.8, 44.4, 41.…- Rappresentare graficamente la distribuzione spaziale (mappa) del pil nelle regioni italiane nei 3 anni considerati. Commentare.
reg2long %>%
ggplot()+
geom_sf(aes(fill=pilprocapite)) +
facet_wrap(~anno) +
scale_fill_gradientn(colors=terrain.colors(20))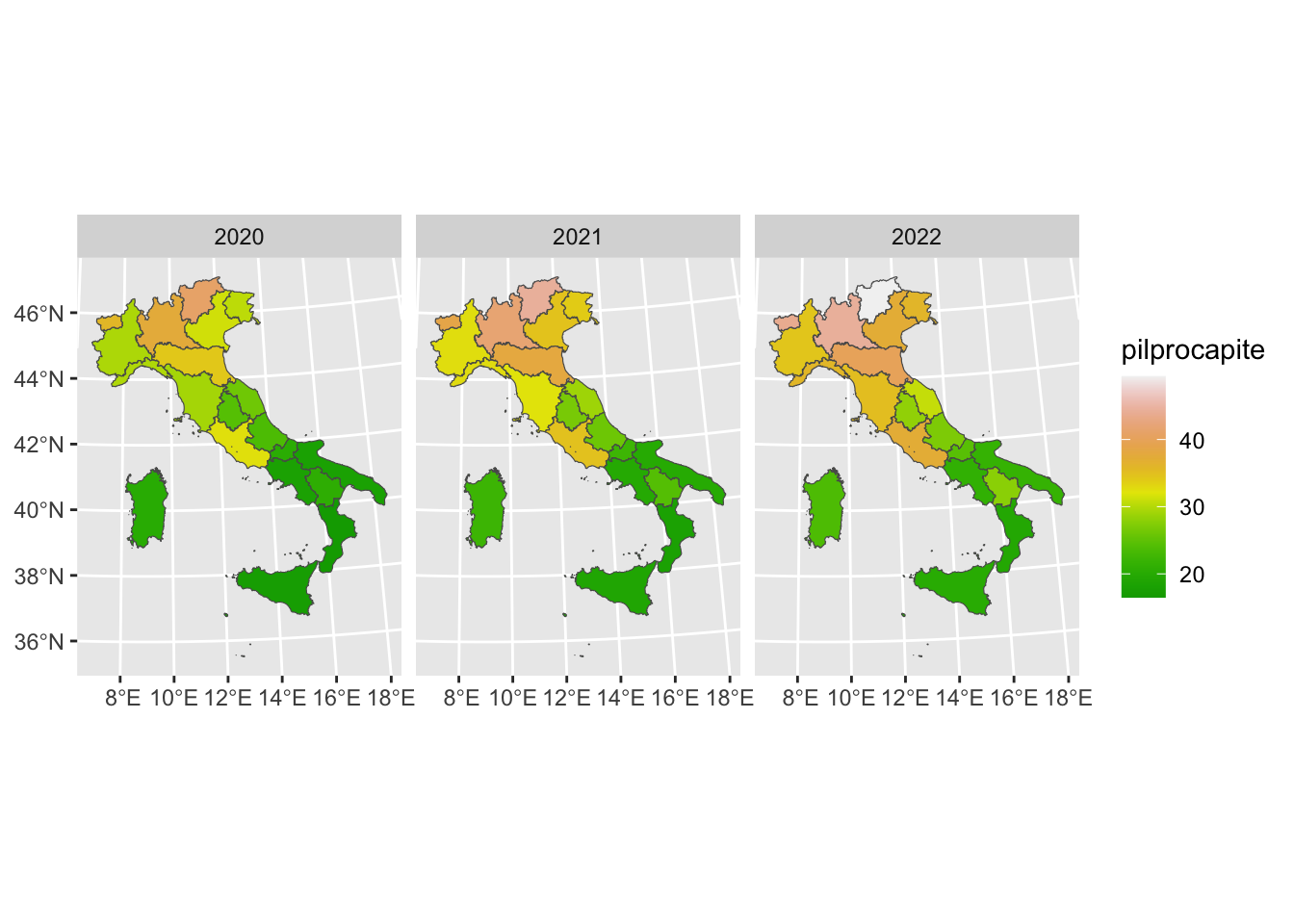 
# Nelle regioni del Nord il pil è più elevato per tutti gli anni considerati
# Si nota un aumento dal 2020 al 2022 dei valori- Rappresentare graficamente la distribuzione del pil nei 3 anni considerati (senza considerare la dimensione spaziale). Commentare.
reg2long %>%
ggplot()+
geom_boxplot(aes(anno, pilprocapite))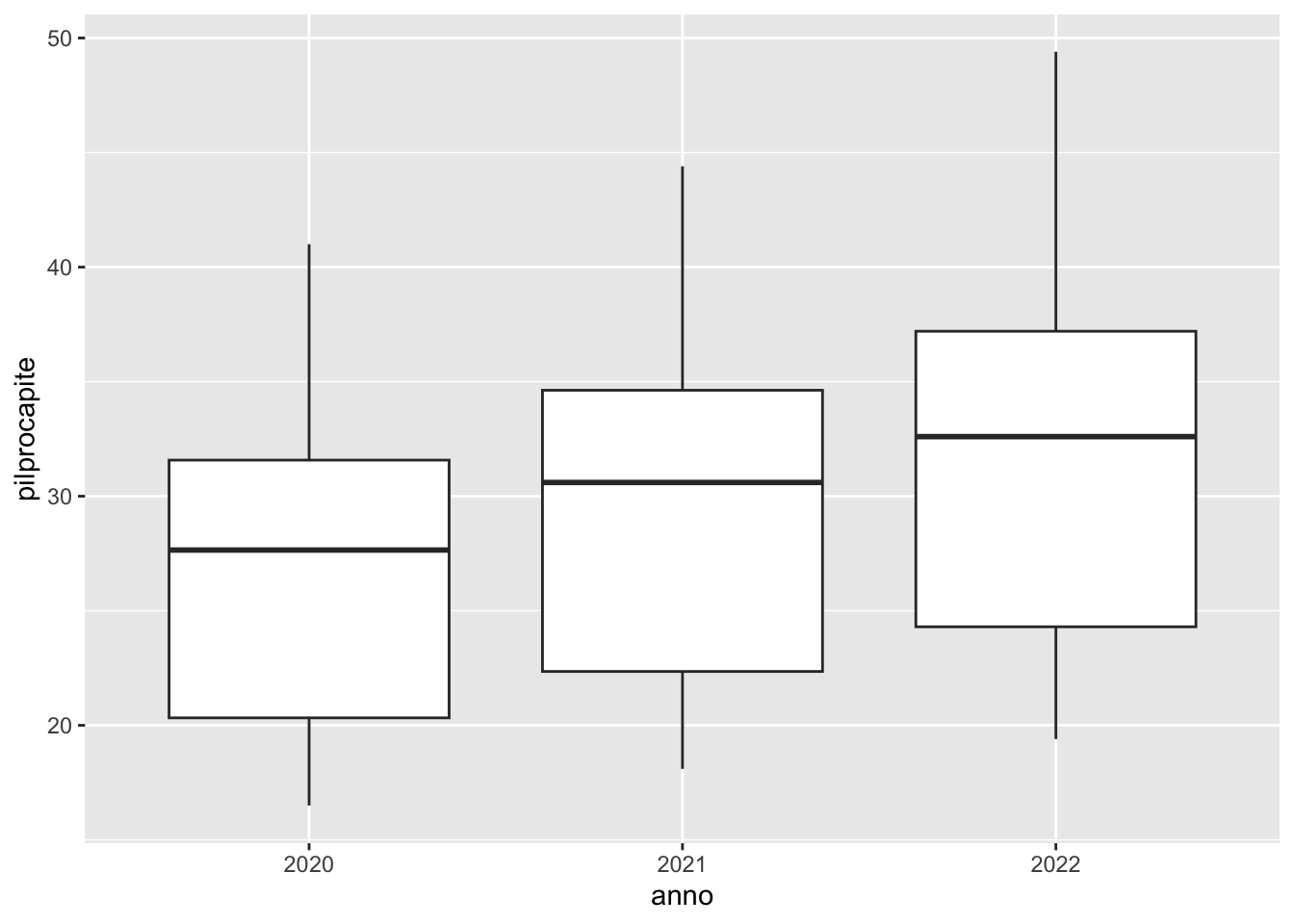 
# Si nota chiaramente un aumento del pil mediano dal 2020 al 2022- Per ogni anno, quale regione ha il pil più elevato? E quale quello minore?
# Pil maggiore
reg2long %>%
group_by(anno) %>%
filter(pilprocapite==max(pilprocapite))Simple feature collection with 3 features and 8 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 606006 ymin: 5059559 xmax: 765957.2 ymax: 5220292
Projected CRS: WGS 84 / UTM zone 32N
# A tibble: 3 × 9
# Groups: anno [3]
COD_RIP COD_REG DEN_REG Shape_Leng Shape_Area TERRITORIO
* <dbl> <dbl> <chr> <dbl> <dbl> <fct>
1 2 4 Trentino-Alto Adige 800894. 13607548167. Trentino-Alto Adi…
2 2 4 Trentino-Alto Adige 800894. 13607548167. Trentino-Alto Adi…
3 2 4 Trentino-Alto Adige 800894. 13607548167. Trentino-Alto Adi…
# ℹ 3 more variables: geometry <MULTIPOLYGON [m]>, anno <chr>,
# pilprocapite <dbl># Pil minore
reg2long %>%
group_by(anno) %>%
filter(pilprocapite==min(pilprocapite))Simple feature collection with 3 features and 8 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 1077562 ymin: 4218139 xmax: 1210849 ymax: 4470355
Projected CRS: WGS 84 / UTM zone 32N
# A tibble: 3 × 9
# Groups: anno [3]
COD_RIP COD_REG DEN_REG Shape_Leng Shape_Area TERRITORIO
* <dbl> <dbl> <chr> <dbl> <dbl> <fct>
1 4 18 Calabria 837811. 15216065606. Calabria
2 4 18 Calabria 837811. 15216065606. Calabria
3 4 18 Calabria 837811. 15216065606. Calabria
# ℹ 3 more variables: geometry <MULTIPOLYGON [m]>, anno <chr>,
# pilprocapite <dbl>- Rappresentare le serie storiche dei valori del pil procapite nel tempo (una linea per ogni regione).
reg2long %>%
ggplot() +
geom_line(aes(anno, pilprocapite,
group=DEN_REG))+
geom_text(aes(anno, pilprocapite, label=ifelse(anno==2022,DEN_REG,NA)),
size=1.5, nudge_x = 0.2)Warning: Removed 40 rows containing missing values or values outside the scale range
(`geom_text()`).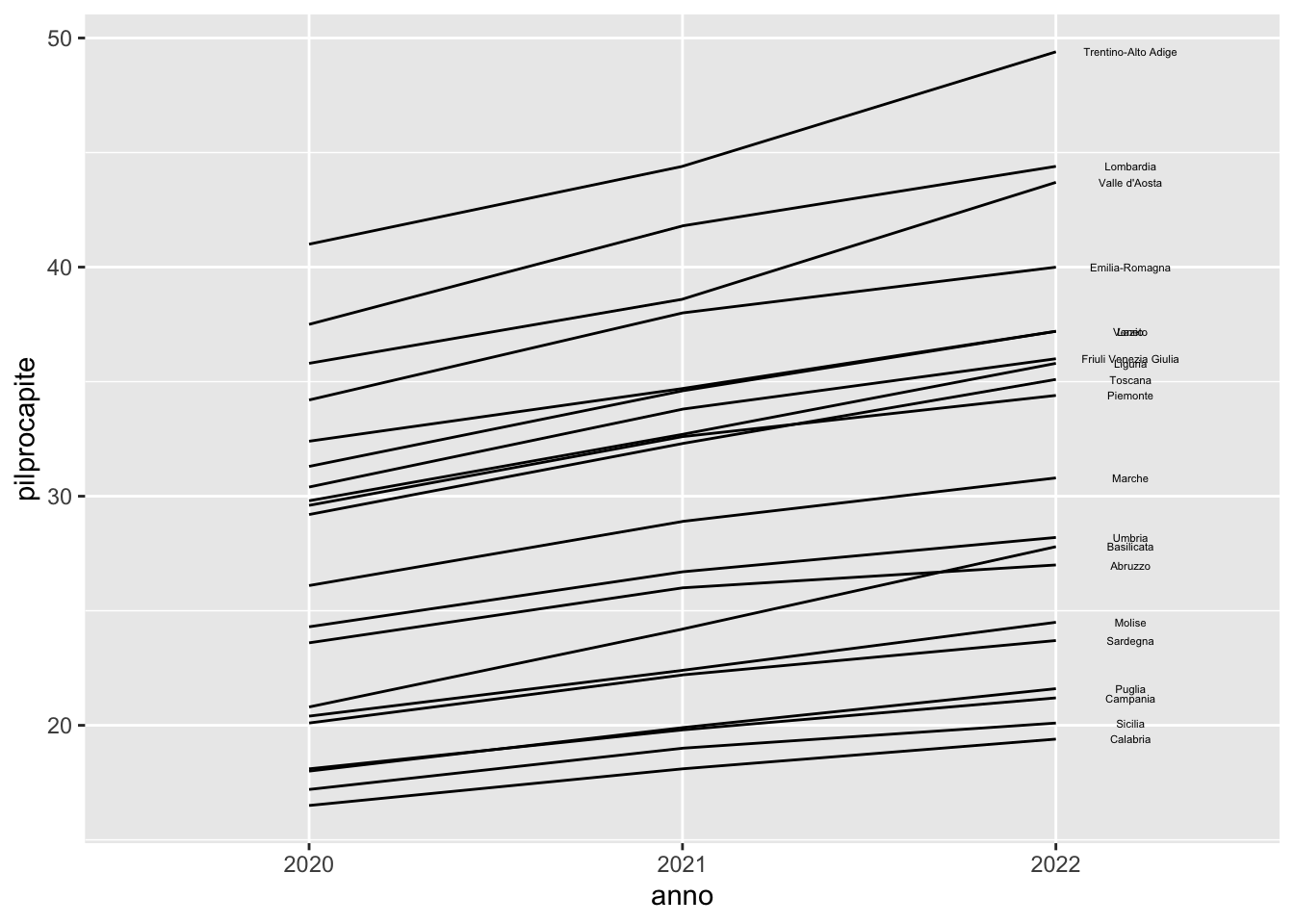
Esercizio 2
Utilizzare i dati Agrimonia (aria) introdotti nel Laboratorio 7.
aria <- read.csv("./data/Agrimonia_Dataset_v_3_0_0.csv",
stringsAsFactors = T)
aria = aria %>%
mutate(Time = ymd(Time))
glimpse(aria)Rows: 309,072
Columns: 43
$ IDStations <fct> 1264, 1264, 1264, 1264, 1264, 1264, 1264, …
$ Latitude <dbl> 46.16785, 46.16785, 46.16785, 46.16785, 46…
$ Longitude <dbl> 9.87921, 9.87921, 9.87921, 9.87921, 9.8792…
$ Time <date> 2016-01-01, 2016-01-02, 2016-01-03, 2016-…
$ Altitude <int> 290, 290, 290, 290, 290, 290, 290, 290, 29…
$ AQ_pm10 <dbl> 62, 73, 44, 31, 27, 27, 43, 37, 48, NaN, N…
$ AQ_pm25 <dbl> 53, 63, 39, 29, 26, 25, 38, 32, 45, NaN, N…
$ AQ_co <dbl> NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, Na…
$ AQ_nh3 <dbl> NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, Na…
$ AQ_nox <dbl> 82.63, 101.70, 66.26, 63.31, 75.53, 61.36,…
$ AQ_no2 <dbl> 37.72, 38.84, 32.34, 31.67, 33.33, 34.40, …
$ AQ_so2 <dbl> NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, Na…
$ WE_temp_2m <dbl> -2.2120, -3.0630, -2.7680, -4.3520, -6.184…
$ WE_wind_speed_10m_mean <dbl> 0.5970, 0.4402, 0.6954, 0.5812, 0.5906, 0.…
$ WE_wind_speed_10m_max <dbl> 0.9883, 0.7365, 1.0100, 0.9421, 0.9847, 1.…
$ WE_mode_wind_direction_10m <fct> S, SE, S, W, SE, S, S, S, SE, SE, NE, S, S…
$ WE_tot_precipitation <dbl> 2.117e-05, 8.282e-03, 2.486e-03, 4.133e-03…
$ WE_precipitation_t <int> 0, 5, 5, 5, 5, 0, 0, 0, 1, 1, 1, 5, 0, 5, …
$ WE_surface_pressure <dbl> 83720, 82990, 82320, 81410, 81530, 81660, …
$ WE_solar_radiation <dbl> 5664000, 1335000, 3728000, 1846000, 173300…
$ WE_rh_min <dbl> 58.11, 75.57, 62.20, 64.27, 58.48, 48.94, …
$ WE_rh_mean <dbl> 74.66, 89.69, 82.27, 83.39, 73.85, 64.94, …
$ WE_rh_max <dbl> 96.33, 96.61, 93.49, 97.39, 95.66, 85.71, …
$ WE_wind_speed_100m_mean <dbl> 1.0730, 1.0530, 1.9810, 1.2080, 0.8226, 1.…
$ WE_wind_speed_100m_max <dbl> 1.977, 2.321, 2.942, 2.284, 1.672, 2.379, …
$ WE_mode_wind_direction_100m <fct> S, S, S, N, SE, SE, S, S, SE, N, N, S, S, …
$ WE_blh_layer_max <dbl> 340.60, 238.70, 407.00, 536.70, 472.40, 59…
$ WE_blh_layer_min <dbl> 10.63, 21.55, 22.80, 12.21, 10.15, 13.31, …
$ EM_nh3_livestock_mm <dbl> 0.2015, 0.2020, 0.2024, 0.2027, 0.2031, 0.…
$ EM_nh3_agr_soils <dbl> 0.1462, 0.1589, 0.1708, 0.1821, 0.1929, 0.…
$ EM_nh3_agr_waste_burn <dbl> 0.0020190, 0.0019560, 0.0018900, 0.0018220…
$ EM_nh3_sum <dbl> 0.6166, 0.6298, 0.6424, 0.6545, 0.6660, 0.…
$ EM_nox_traffic <dbl> 0.8359, 0.8372, 0.8384, 0.8396, 0.8409, 0.…
$ EM_nox_sum <dbl> 1.720, 1.720, 1.720, 1.720, 1.720, 1.721, …
$ EM_so2_sum <dbl> 0.3906, 0.3911, 0.3916, 0.3923, 0.3931, 0.…
$ LI_pigs <dbl> 0.3832, 0.3832, 0.3832, 0.3832, 0.3832, 0.…
$ LI_bovine <dbl> 5.892, 5.892, 5.892, 5.892, 5.892, 5.892, …
$ LI_pigs_v2 <fct> 4.167e-01, 4.167e-01, 4.168e-01, 4.168e-01…
$ LI_bovine_v2 <fct> 6.467e+00, 6.463e+00, 6.458e+00, 6.454e+00…
$ LA_hvi <dbl> 3.998, 3.997, 3.997, 3.997, 3.997, 3.996, …
$ LA_lvi <dbl> 1.234, 1.234, 1.234, 1.234, 1.233, 1.233, …
$ LA_land_use <int> 112, 112, 112, 112, 112, 112, 112, 112, 11…
$ LA_soil_use <int> 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17…- Si consideri la variabile
WE_temp_2m(temperatura). Rappresentare graficamente la serie storica giornaliera della temperatura (dal 2016 al 2021) per la stazione di monitoraggio 706
aria %>%
filter(IDStations==706) %>%
ggplot() +
geom_line(aes(Time,WE_temp_2m))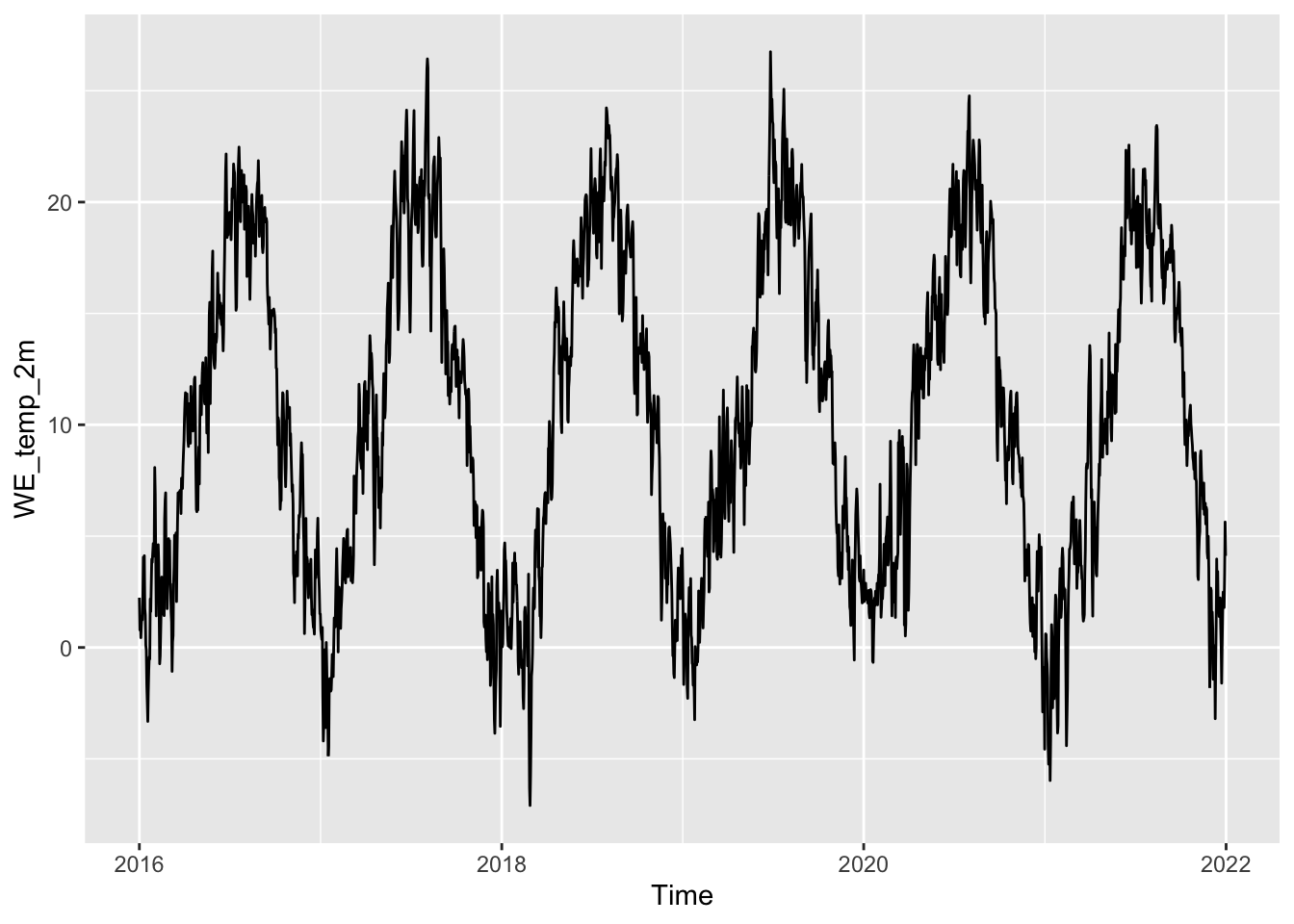
- Calcolare la temperatura media e mediana separatamente per ogni anno per la stazione 706.
aria %>%
filter(IDStations==706) %>%
group_by(year(Time)) %>%
summarise(media=mean(WE_temp_2m),
mediana=median(WE_temp_2m))# A tibble: 6 × 3
`year(Time)` media mediana
<dbl> <dbl> <dbl>
1 2016 10.2 10.2
2 2017 10.4 11.0
3 2018 10.7 11.7
4 2019 10.7 9.96
5 2020 10.6 10.9
6 2021 9.69 9.37- Considerare solo l’ultimo anno disponibile (2021). Calcolare per ogni stazione la temperatura media annua (usare come nome della variabile
mediatemp).
ariam = aria %>%
filter(year(Time)==2021) %>%
group_by(IDStations, Longitude, Latitude) %>%
summarise(mediatemp=mean(WE_temp_2m, na.rm=T))`summarise()` has grouped output by 'IDStations', 'Longitude'. You can override
using the `.groups` argument.glimpse(ariam)Rows: 141
Columns: 4
Groups: IDStations, Longitude [141]
$ IDStations <fct> 1264, 1265, 1266, 1269, 1274, 1297, 1374, 1800, 1801, 501, …
$ Longitude <dbl> 9.879210, 9.495274, 9.666250, 9.601223, 9.286409, 9.930596,…
$ Latitude <dbl> 46.16785, 45.30278, 45.23349, 45.64970, 46.01583, 45.15047,…
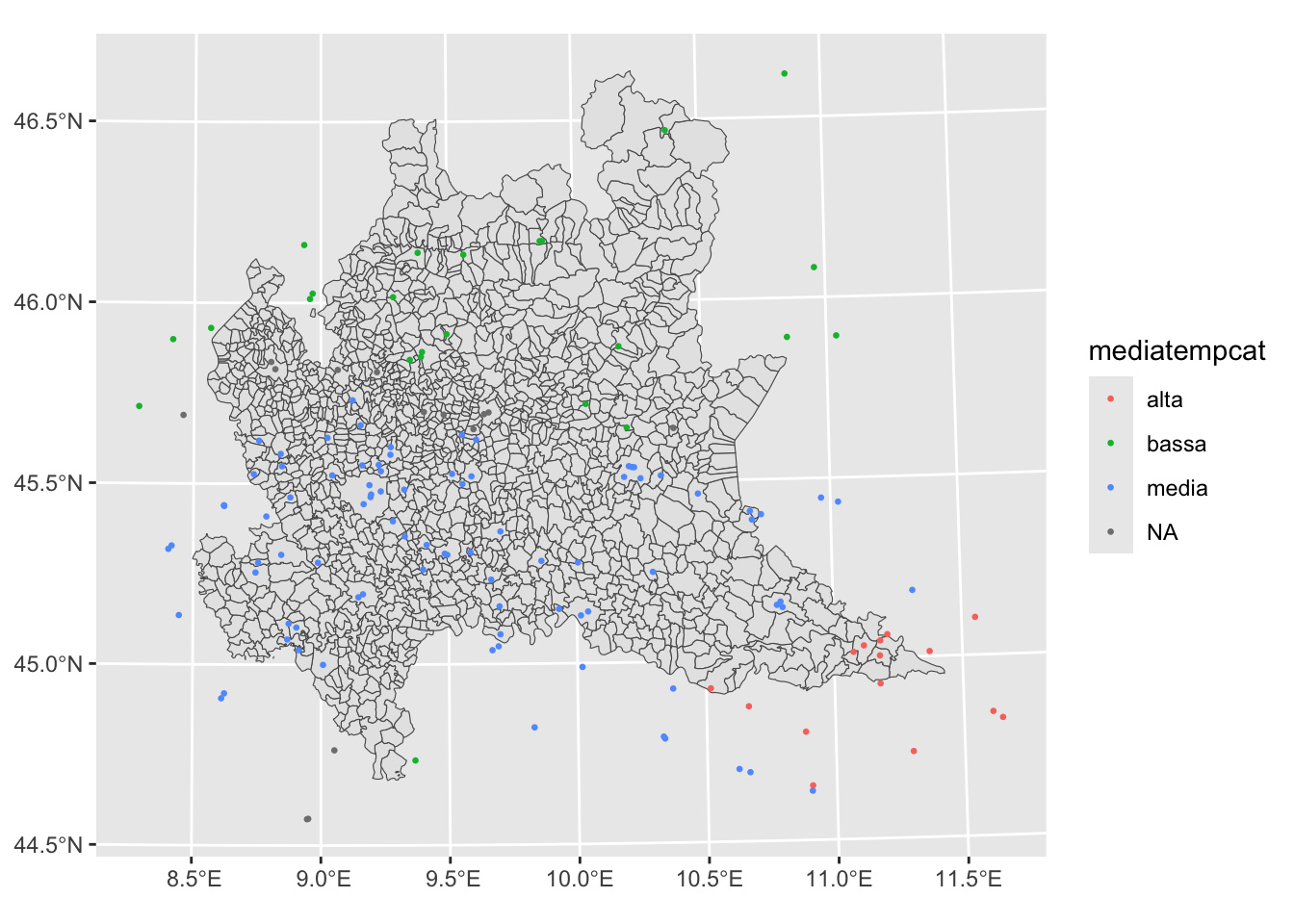
$ mediatemp <dbl> 3.126110, 13.548991, 13.767447, 11.936187, 9.065756, 13.862…- Usando
case_when(si veda Section 4.4.4) ricodificare la variabile quantitativa continuamediatempin una variabile categoriale (mediatempcat) con 3 modalità (bassa, media e alta) secondo le seguenti regole:
mediatempcatassume categoria “bassa” semediatempè minore di 11 gradi,mediatempcatassume categoria “media” semediatempè compresa tra 12 e 14 gradi (si consiglia in questo caso di usarebetween(mediatemp,12,14)),mediatempcatassume categoria “alta” semediatempè maggiore di 14 gradi.
La nuova variabile mediatempcat va aggiunta al data frame creato al punto precedente.
ariam = ariam %>%
mutate(mediatempcat = case_when(
mediatemp < 11 ~ "bassa",
between(mediatemp, 12, 14) ~ "media",
mediatemp > 14 ~ "alta",
))
glimpse(ariam)Rows: 141
Columns: 5
Groups: IDStations, Longitude [141]
$ IDStations <fct> 1264, 1265, 1266, 1269, 1274, 1297, 1374, 1800, 1801, 501…
$ Longitude <dbl> 9.879210, 9.495274, 9.666250, 9.601223, 9.286409, 9.93059…
$ Latitude <dbl> 46.16785, 45.30278, 45.23349, 45.64970, 46.01583, 45.1504…
$ mediatemp <dbl> 3.126110, 13.548991, 13.767447, 11.936187, 9.065756, 13.8…
$ mediatempcat <chr> "bassa", "media", "media", NA, "bassa", "media", "media",…- Rappresentare nella mappa dei comuni della Lombardia le stazioni di monitoraggio colorando i punti in base alla temperatura media categoriale (
mediatempcat) creata al punto precedente.
reglomb = st_read("./data/lombardia_com.shp")Reading layer `lombardia_com' from data source
`/Users/michelacameletti/Library/CloudStorage/GoogleDrive-michela.cameletti@unibg.it/My Drive/UniBg/Didattica/Lingue_GeoUrb/2023-2024/MAD2324Rlabs/data/lombardia_com.shp'
using driver `ESRI Shapefile'
Simple feature collection with 1506 features and 12 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 460662.8 ymin: 4947430 xmax: 691489.7 ymax: 5165371
Projected CRS: WGS 84 / UTM zone 32Nariamsf = st_as_sf(ariam,
coords = c("Longitude","Latitude"),
crs = st_crs("WGS84")) %>%
st_transform(st_crs(reglomb))
ariamsf %>%
ggplot() +
geom_sf(data=reglomb) +
geom_sf(aes(col=mediatempcat), cex=0.5) 