dati = read.csv("./data/DatiCom.csv")5 Lab 4 - 22/03/2024
In questa lezione vedremo:
continueremo ad utilizzare i verbi del pacchetto
dplyr(parte della collezionetidyverse),andremo a realizzare i primi grafici con il pacchetto
ggplot(parte della collezionetidyverse).
Verranno nuovamente utilizzati i dati disponibili nel file DatiCom.csv già in uso nel Chapter 4.
Come prima cosa è necessario caricare il pacchetto tidyverse (come descritto in Section 4.2):
library(tidyverse)── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.4
✔ forcats 1.0.0 ✔ stringr 1.5.0
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.2 ✔ tidyr 1.3.0
✔ purrr 1.0.2
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors5.1 Rappresentazioni grafiche tramite ggplot
All’interno della collezione tidyverse è disponibile il pacchetto ggplot (Grammar of Graphics) che permette di ottenere rappresentazioni grafiche (https://ggplot2.tidyverse.org/). Come si vede in Figure 5.1 ggplot costruisce il grafico tramite una serie di layer. Il primo livello specifica il sistema di coordinate; successivamente vengono aggiunti gli altri layer caratterizzata da una specifica geometria (geom_...) e caratteristiche estetiche (aes(...)).
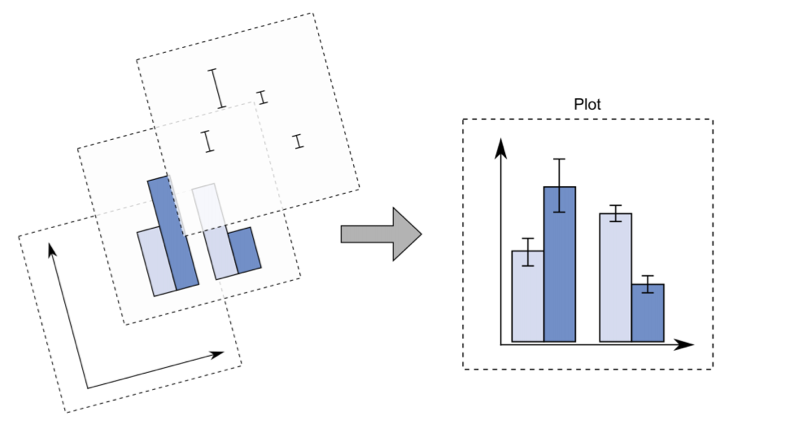
ggplotOgni costruzione di grafico avrà la seguente struttura:
dati %>%
ggplot() +
geom_...(aes(…))ggplot è la funzione che crea il sistema di coordinate. La funzione geom_... è quella che definisce la geometria da rappresentare graficamente (vedere https://ggplot2.tidyverse.org/reference/ per l’elenco di tutte le geometrie disponibili). Infine, aes definisce tutto quello che è importante per l’estetica del grafico (incluse le variabili da rappresentare).
Importante: si noti che dopo ggplot non si utilizza più il pipe (%>%) ma il segno di +.
5.1.1 Geometria geom_bar
Si consideri la variabile zona_alt (eventualmente ricodificata in zona_alt2 come descritto in Section 4.4.4) e se ne ricavi nuovamente la distribuzione di frequenza (si veda anche Section 4.4.1):
dati %>%
count(zona_alt) zona_alt n
1 1 2370
2 2 117
3 3 2530
4 4 785
5 5 2098Rappresentiamo ora graficamente questa distribuzione di frequenza con un grafico a barre che riporta sull’asse delle x le categorie della variabile e sull’asse delle coordinate le corrispondenti frequenze assolute. Questo tipo di grafico può essere utilizzato per una variabile qualitativa o quantitativa che assume un numero finito di valori. Si utilizza il codice che segue usando la geometria geom_bar:
dati %>%
ggplot()+
geom_bar(aes(zona_alt))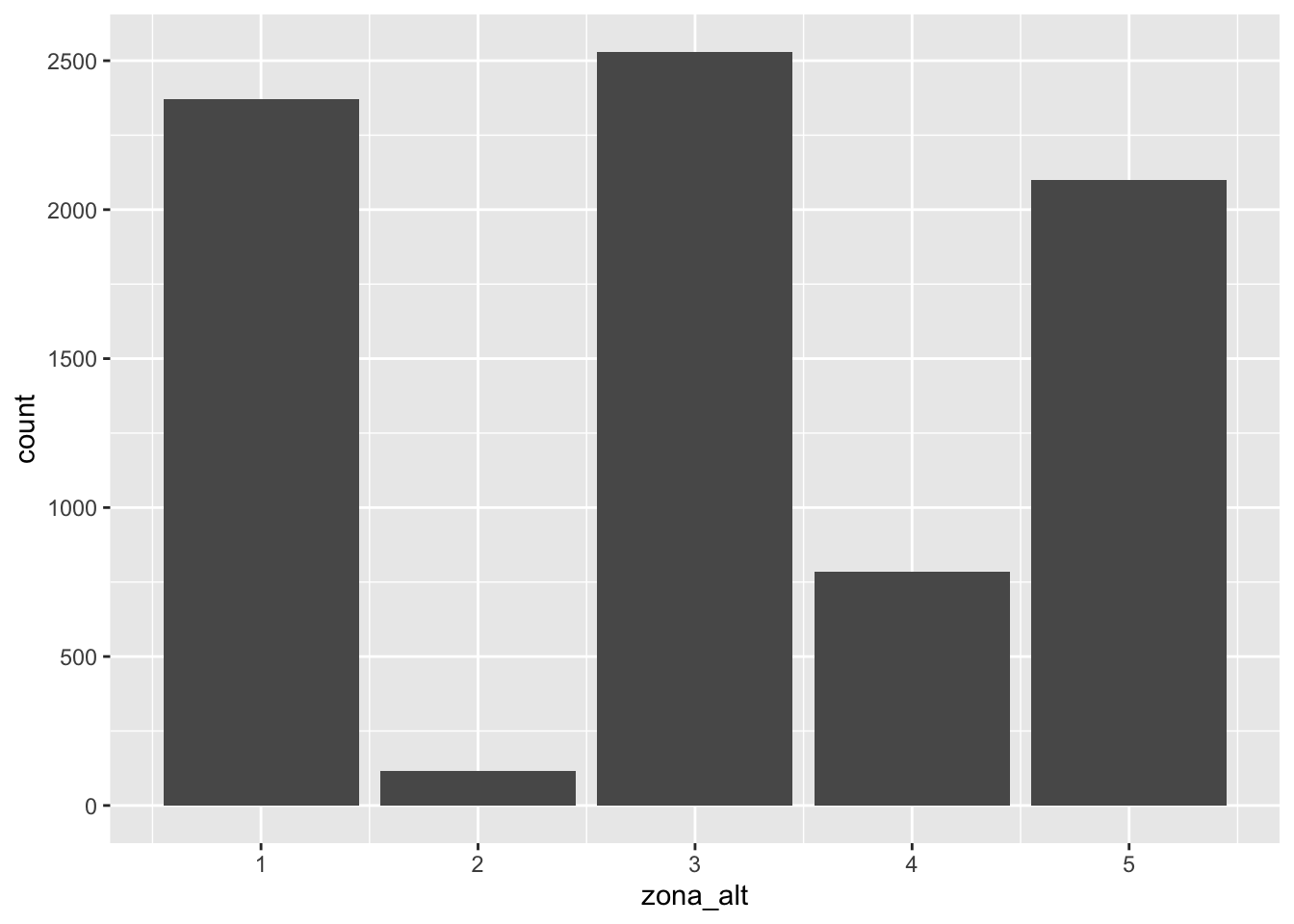
In automatico il grafico riporta sull’asse delle y la variabile count che rappresenta la frequenza assoluta, ovvero il numero di comuni per ognuna delle 5 categorie di zona_alt. E’ possibile cambiare i colori esterni (col) e interni (fill) di ogni barra come segue (usando le opzioni col e fill:
dati %>%
ggplot()+
geom_bar(aes(zona_alt), col="blue", fill="orange")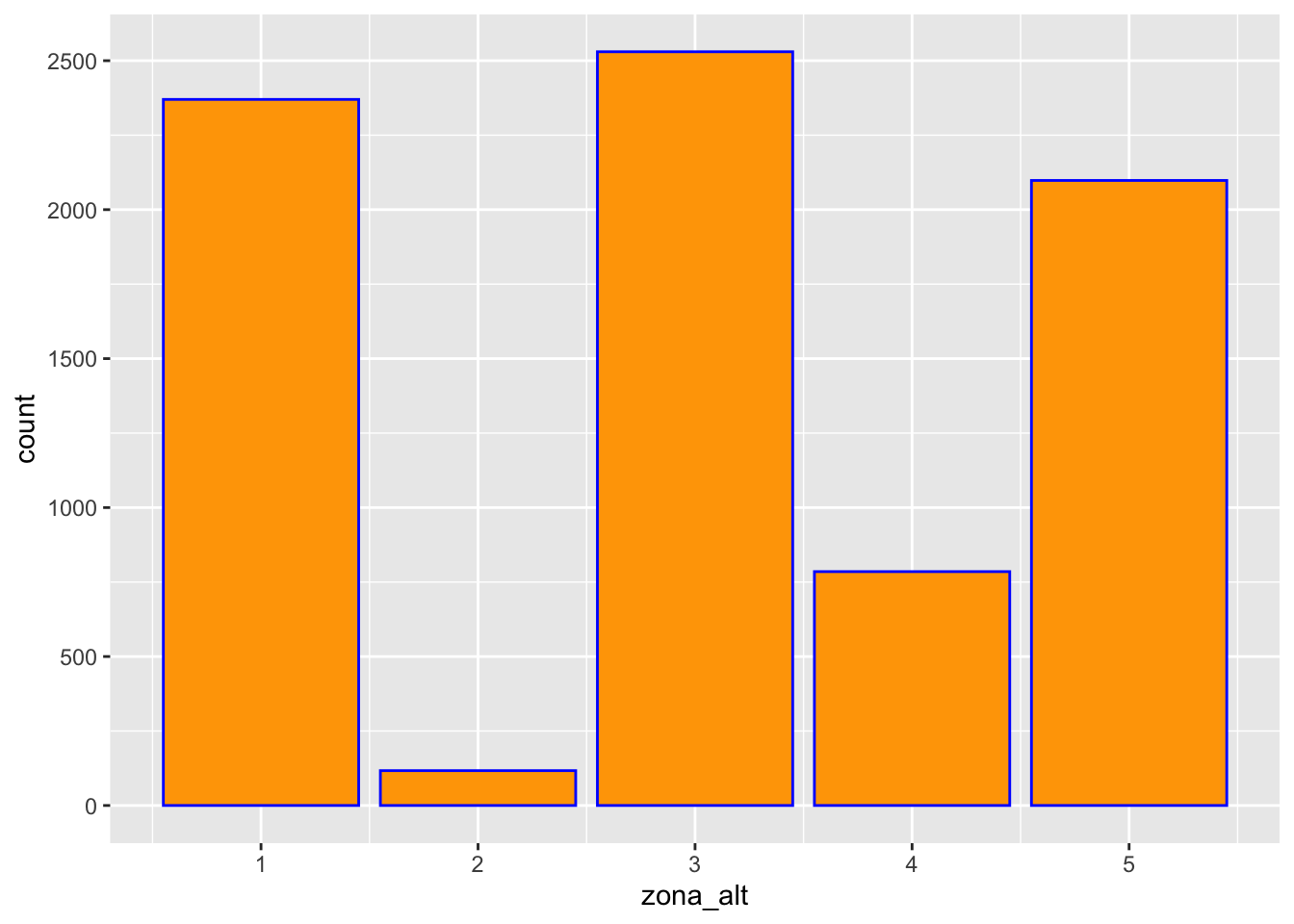
# dentro aes si specifica solo la variabile xPer cambiare le etichette dei due assi si utilizzano le funzioni xlab e ylab come segue (vengono anche usati colori diversi):
dati %>%
ggplot() +
geom_bar(aes(zona_alt), col = "darkgreen", fill = "#FF9999") +
xlab("Zona altimetrica") +
ylab("Frequenze assolute")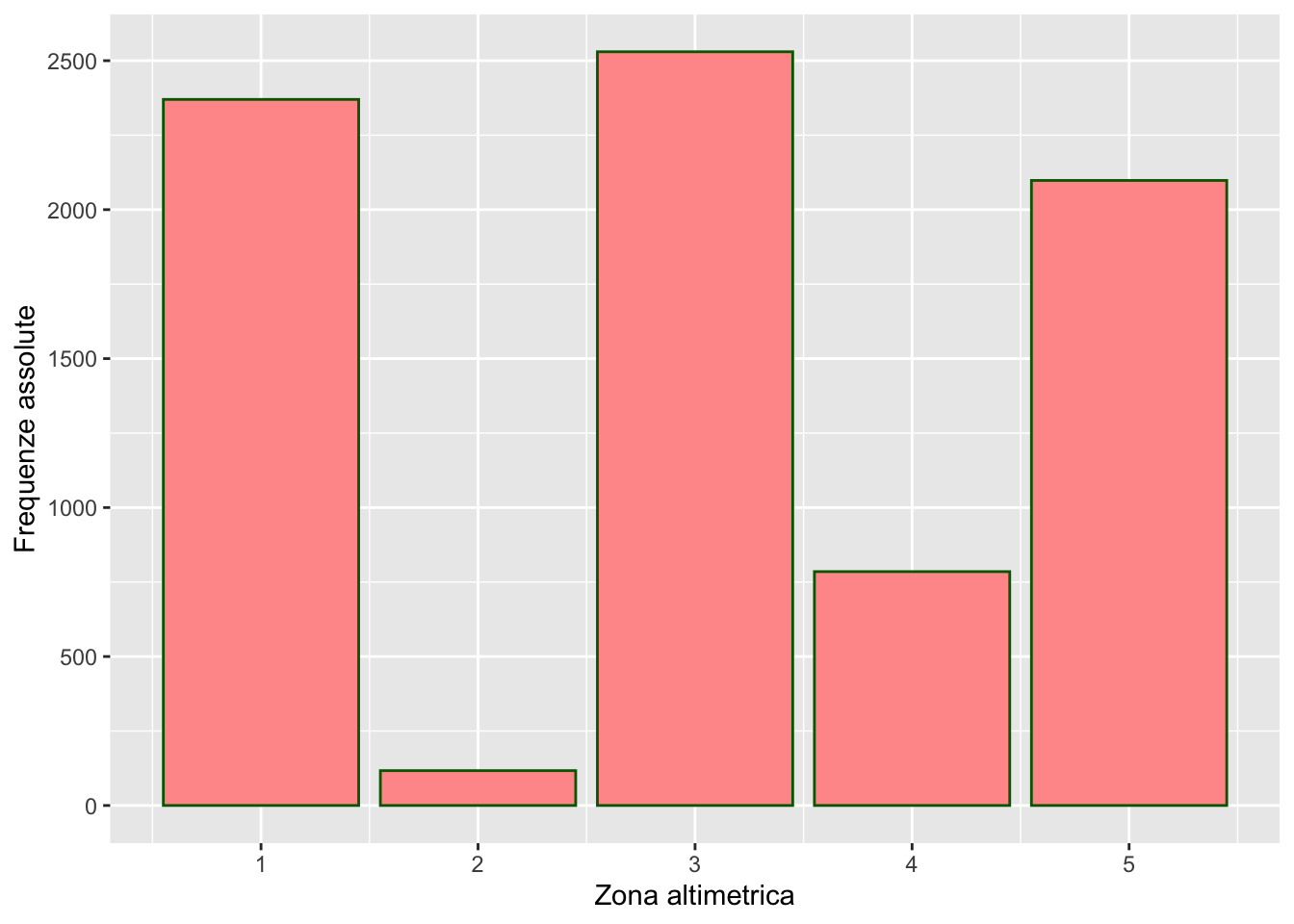
5.1.2 Geometria geom_col
Si voglia ora rappresentare sull’asse delle y non le frequenze assolute (come fatto in automatico da geom_bar) ma le frequenze percentuali (si veda Section 3.2). In questo caso è necessario utilizzare la geometrica geom_col che permette di specificare cosa si vuole rappresentare sull’asse delle y. I dati di input del grafico non sarà il dataframe originale dati ma la seguente tabella di distribuzioni di frequenza con le distribuzioni percentuali denominate perc:
dati %>%
count(zona_alt) %>%
mutate(perc = n/sum(n)*100) zona_alt n perc
1 1 2370 30.000000
2 2 117 1.481013
3 3 2530 32.025316
4 4 785 9.936709
5 5 2098 26.556962Per il grafico si procede come segue:
dati %>%
count(zona_alt) %>%
mutate(perc = n/sum(n)*100) %>%
ggplot() +
geom_col(aes(zona_alt, perc))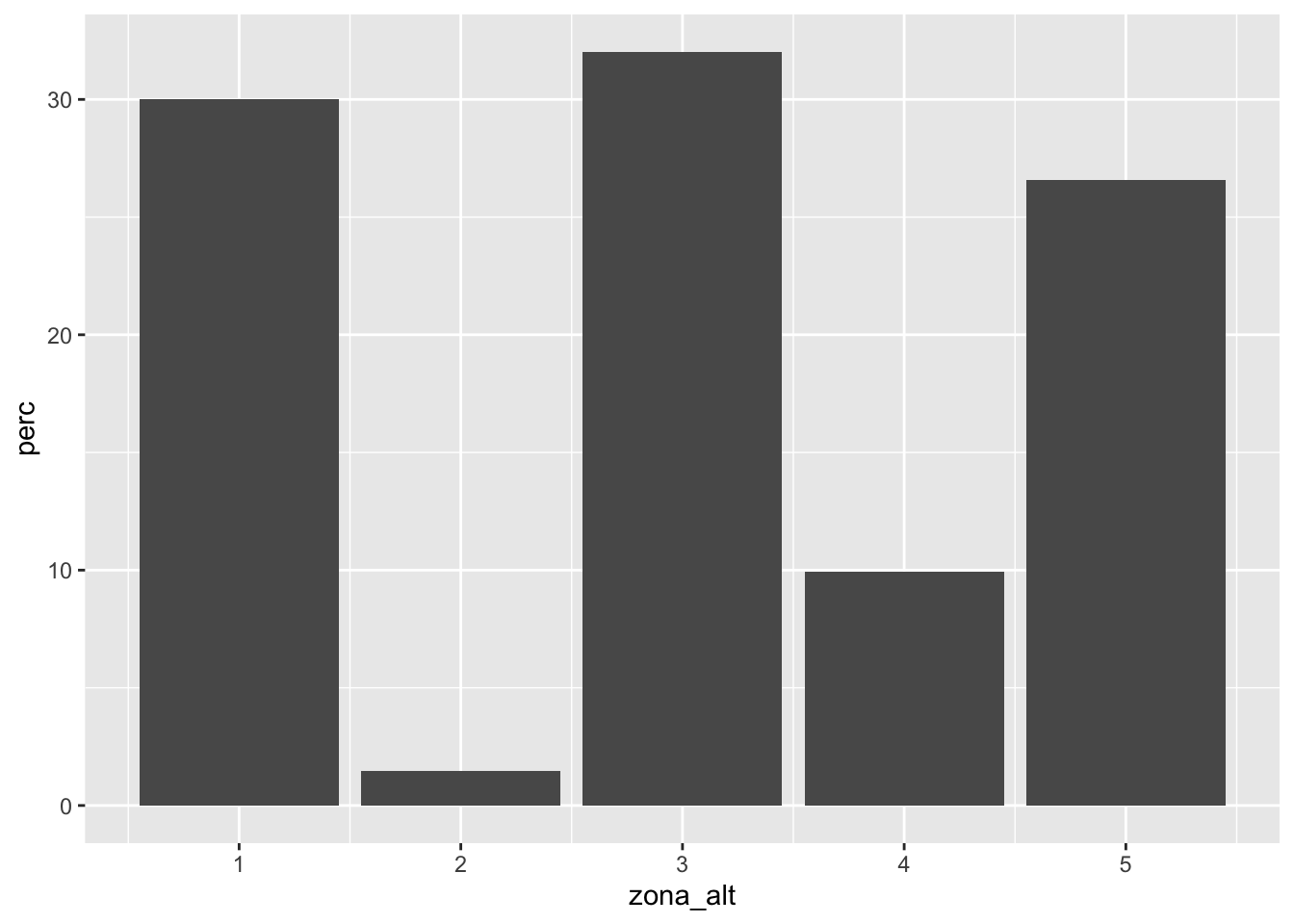
Quello che cambia è la scala dell’asse delle y. Si voglia ora migliorare il grafico andando a mettere un bordo rosso alle colonne e un riempimento di colore dato dai valori delle percentuali (variabile perc). In questo caso l’opzione col andrà specificata dentro aes() (e senza mettere il colore scelto nelle virgolette; il colore è definito dalla variabile perc) come segue:
dati %>%
count(zona_alt) %>%
mutate(perc = n/sum(n)*100) %>%
ggplot() +
geom_col(aes(zona_alt, perc, fill=perc),
col = "red") +
xlab("Zona altimetrica") +
ylab("Frequenze percentuali")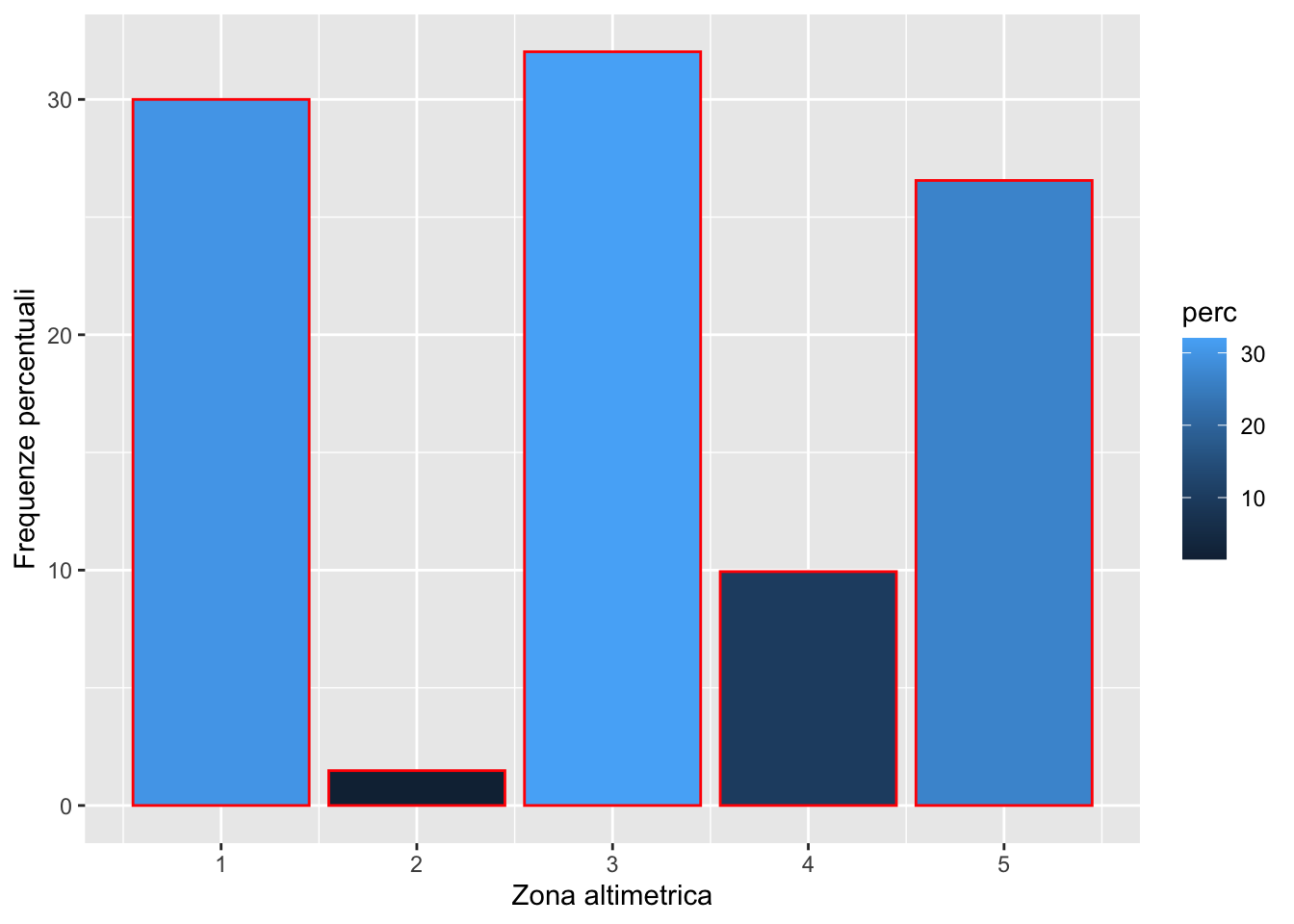
Si noti la creazione automatica della legenda con paletta da blu scuro (valori percentuali bassi) a blu chiaro (valori percentuali alti). E’ possibile cambiare la palette di colori come segue (si veda anche https://ggplot2.tidyverse.org/reference/scale_colour_continuous.html):
dati %>%
count(zona_alt) %>%
mutate(perc = n/sum(n)*100) %>%
ggplot() +
geom_col(aes(zona_alt, perc, fill = perc), col = "red") +
scale_fill_continuous(type = "viridis") +
xlab("Zona altimetrica") +
ylab("Frequenze percentuali")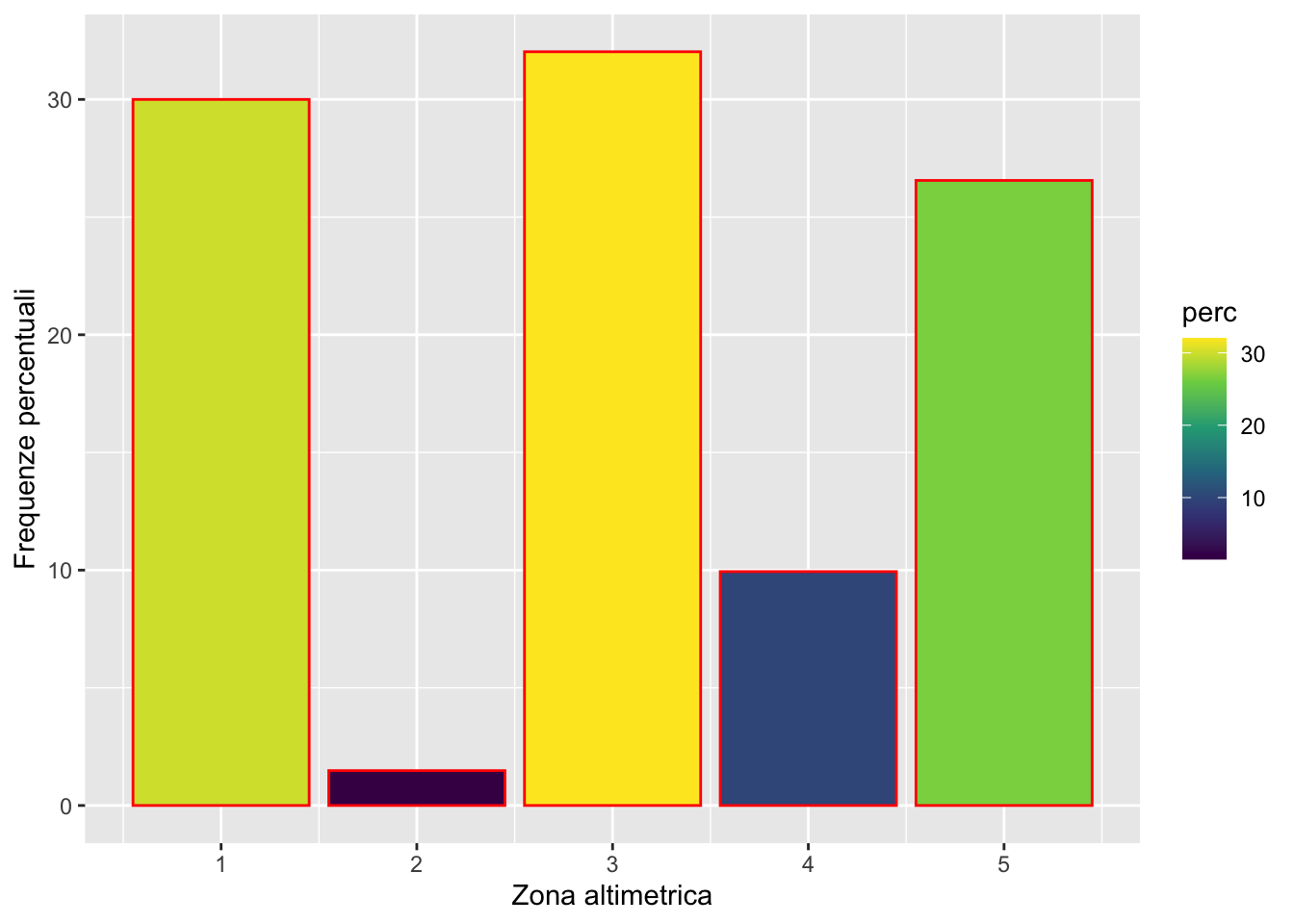
5.2 Verbo filter
Il verbo filter viene utilizzato per selezionare righe (osservazioni) da un dataframe (andando a stabiliare una condizione per la selezione).
Si voglia ad esempio selezionare solamente i comuni in Lombardia (codreg == 3) e creare un nuovo dataframe di nome datilomb:
datilomb = dati %>%
filter(codreg == 3) #esattamente uguale
nrow(datilomb)[1] 1503Si noti che in Lombardia sono presenti 1503 comuni. Le variabili (colonne) sono le stesse di dati.
Si voglia ora selezionare solo il comune di Bergamo dentro datilomb:
datilomb %>%
filter(nomecom == "Bergamo") codreg codcom nomecom sup pop zona_alt alt lito isol cost urban
1 3 16024 Bergamo 40.15 119534 3 249 0 0 0 15.2.1 Calcolo indici descrittivi
A partire da datilomb si calcoli per la variabile pop il minimo, il massimo, la media, la varianza e il coefficiente di variazone.
- Metodo classico
min(datilomb$pop) #n. persone residenti nel comune con meno abitanti[1] 32max(datilomb$pop) #n. persone residenti nel comune con più abitanti (Milano)[1] 1354196mean(datilomb$pop) #n. medio di persone residenti nei comuni lombardi[1] 6620.587var(datilomb$pop) #variabilità della variabile pop: quanto sono diversi i comuni di lombardia in termini di popolazione?[1] 1325944151#CV
sd(datilomb$pop)/mean(datilomb$pop)[1] 5.500044- Metodo
tidyverse
datilomb %>%
summarise(min(pop), max(pop), mean(pop), var(pop), sd(pop)/mean(pop)) min(pop) max(pop) mean(pop) var(pop) sd(pop)/mean(pop)
1 32 1354196 6620.587 1325944151 5.500044Se si è interessati a capire quale è il comune con la popolazione minima (32 persone) si usi filter:
datilomb %>%
filter(pop == 32) codreg codcom nomecom sup pop zona_alt alt lito isol cost urban
1 3 97055 Morterone 13.71 32 1 1070 0 0 0 3Il codice
datilomb %>%
filter(pop < 50) codreg codcom nomecom sup pop zona_alt alt lito isol cost urban
1 3 14047 Pedesina 6.30 37 1 1032 0 0 0 3
2 3 18125 Rocca de' Giorgi 10.50 49 3 219 0 0 0 3
3 3 97055 Morterone 13.71 32 1 1070 0 0 0 3ci dice quale sono i comuni in Lombardia con un numero di abitanti minore di 50.
5.3 Geometria geom_histogram
Volendo rappresentare graficamente una variabile quantitativa continuo o discreta con un numero elevato di categorie, come ad esempio la popolazione, si utilizza l’istogramma (geometria geom_histogram):
datilomb %>%
ggplot() +
geom_histogram(aes(pop))`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.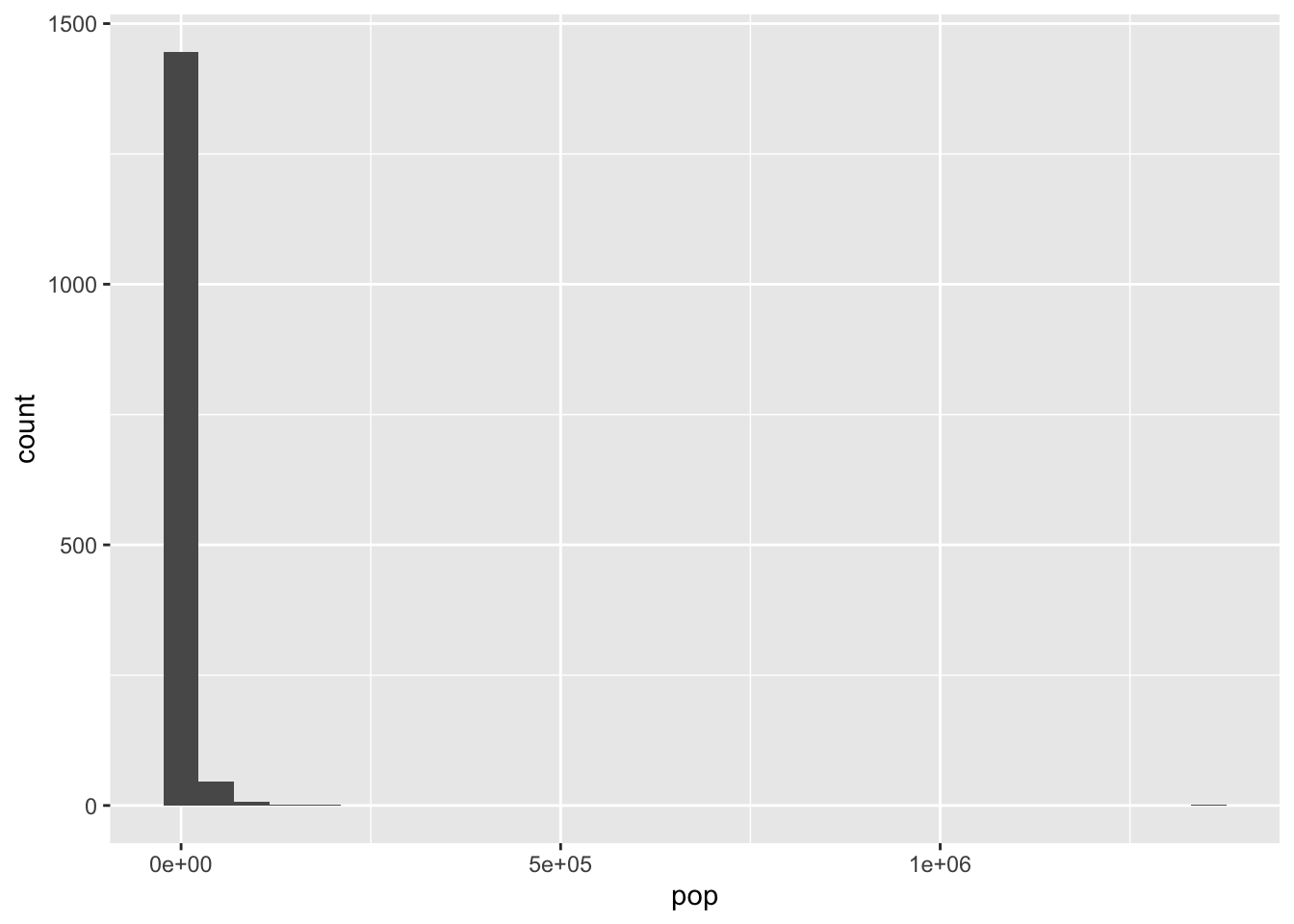
L’istogramma riporta sull’asse delle x i valori della popolazione in classi (definite in automatico da R) e sull’asse delle y le corrispondente frequenze (i.e. numero di comuni lombardi). Sull’asse delle ordinate viene infatti riportato il conteggio (count), ovvero quante osservazioni ci sono per ogni classe di popolazione. In automatico il numero di classi (bins) per i prezzi sono fissate pari a 30. E’ comunque possibile scegliere il numero di classi con l’opzione bins=.... Si noti che molti comuni hanno una popolazione ridotta (nella prima classe di valori), il comune di Milano è quello che si vede nella parte di destra del codice.
Essendo Milano un’anomalia lo si vuole escludere (con filter applicato alla variable nomecom) prima di fare il grafico:
datilomb %>%
filter(nomecom != "Milano") %>%
ggplot() +
geom_histogram(aes(pop), col="darkblue") +
xlab("Popolazione residente (in classi)") +
ylab("Frequenze assolute")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.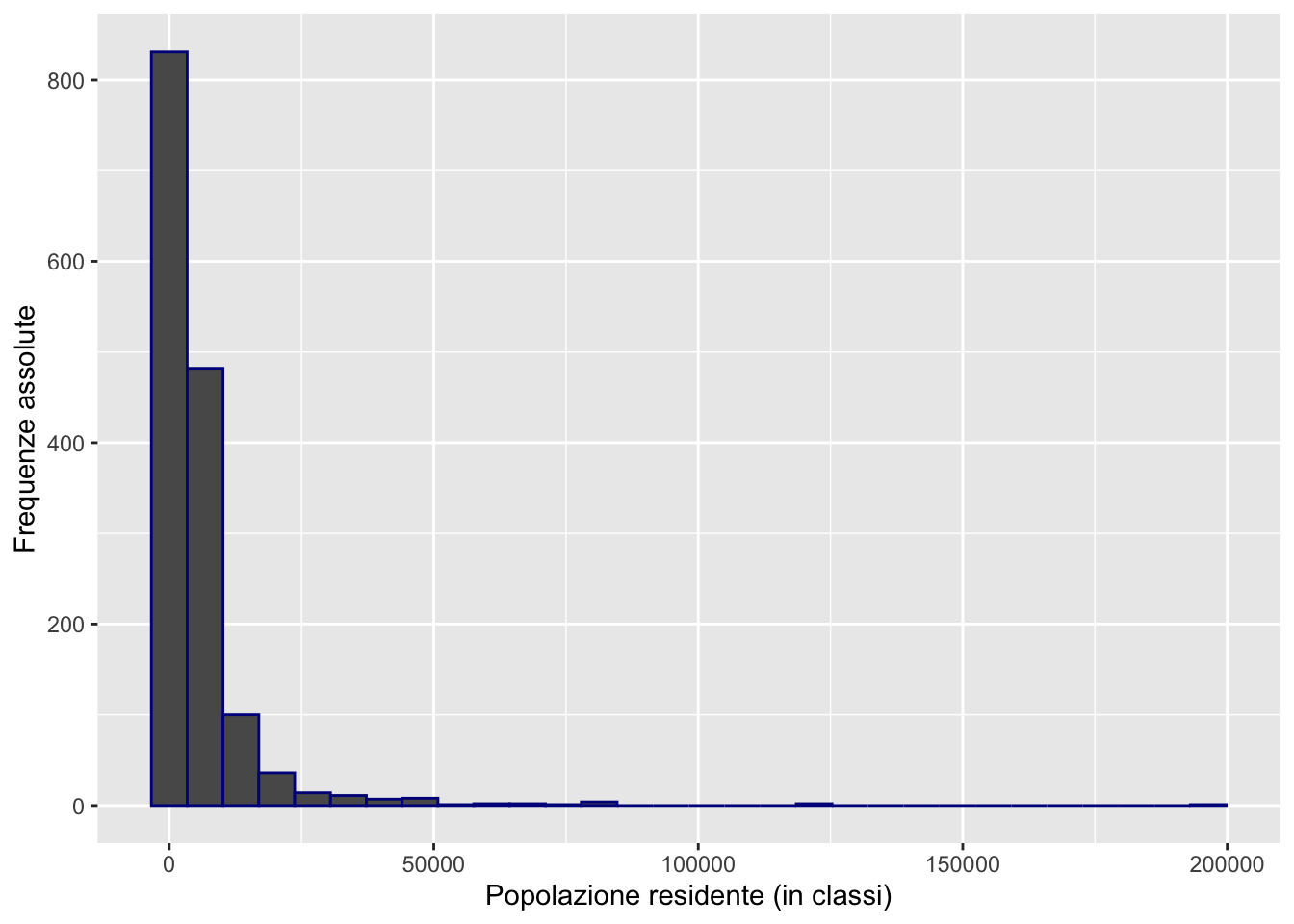
Il simbolo != significa diverso da. SI vede che ora l’asse delle x arriva a 200000. Ancora la maggior parte dei comuni è collocata nella parte di destra del grafico.
5.3.1 facet_wrap
Vogliamo ora creare istogrammi per la variabile popolazione separati a seconda delle categorie della zona altimetrica (zona_alt). Si può includere questa informazione settando l’opzione fill con zon_alt trasformato in factor dentro l’aes (vedremo meglio più avanti la questione dei factor):
datilomb %>%
filter(nomecom != "Milano") %>%
ggplot() +
geom_histogram(aes(pop, fill = factor(zona_alt)), col="darkblue") +
xlab("Popolazione residente (in classi)") +
ylab("Frequenze assolute")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.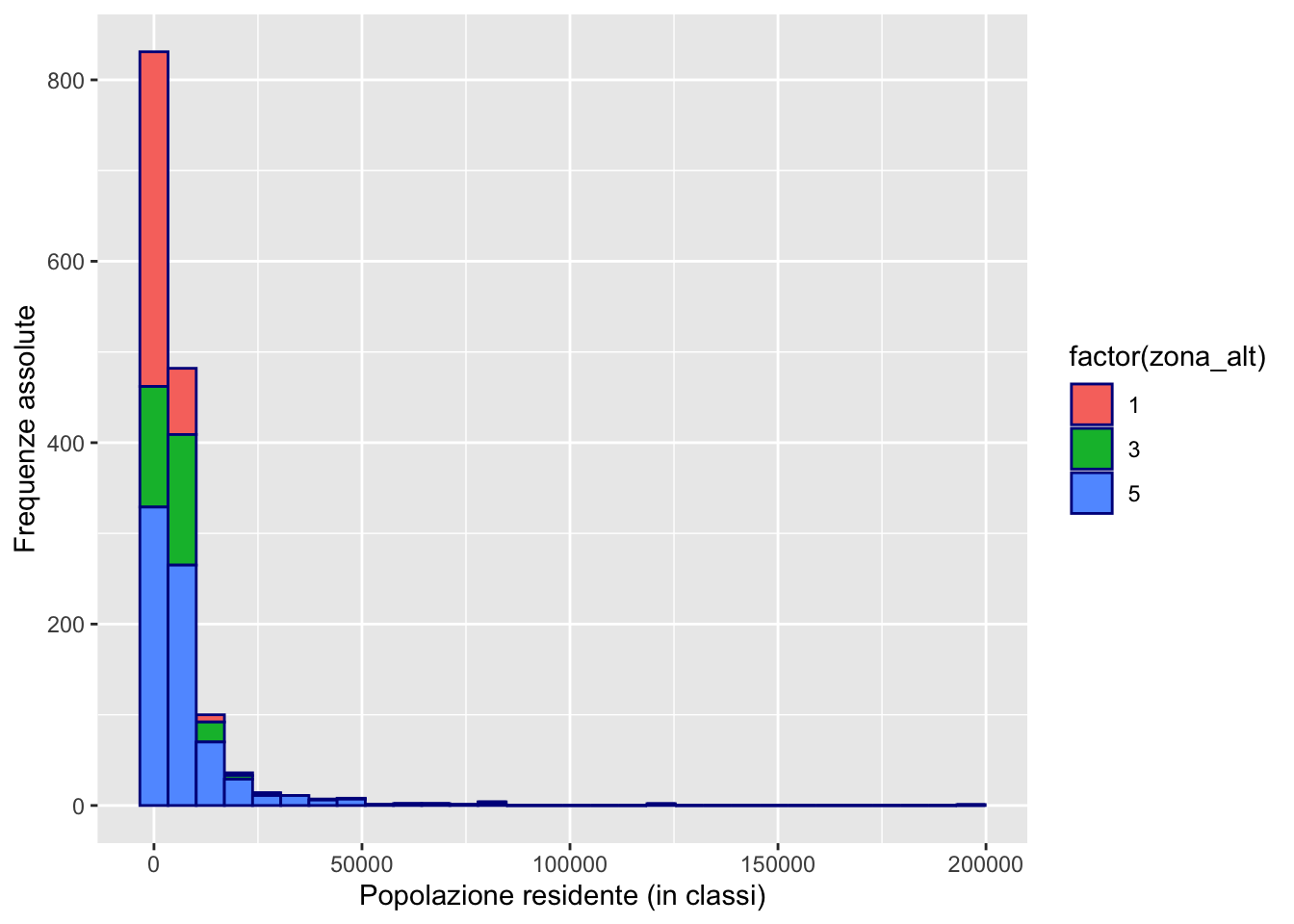
In questo caso i 3 istogrammi sono sovrapposti (con colori diversi) e poco leggibili. Sarebbe meglio separare i 3 istogrammi in 3 sotto-grafici diversi. E’ possibile farlo usando la funzione facet_wrap: avere
datilomb %>%
filter(nomecom != "Milano") %>%
ggplot() +
geom_histogram(aes(pop, fill = factor(zona_alt)), col="darkblue") +
facet_wrap(~ zona_alt) +
xlab("Popolazione residente (in classi)") +
ylab("Frequenze assolute") `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.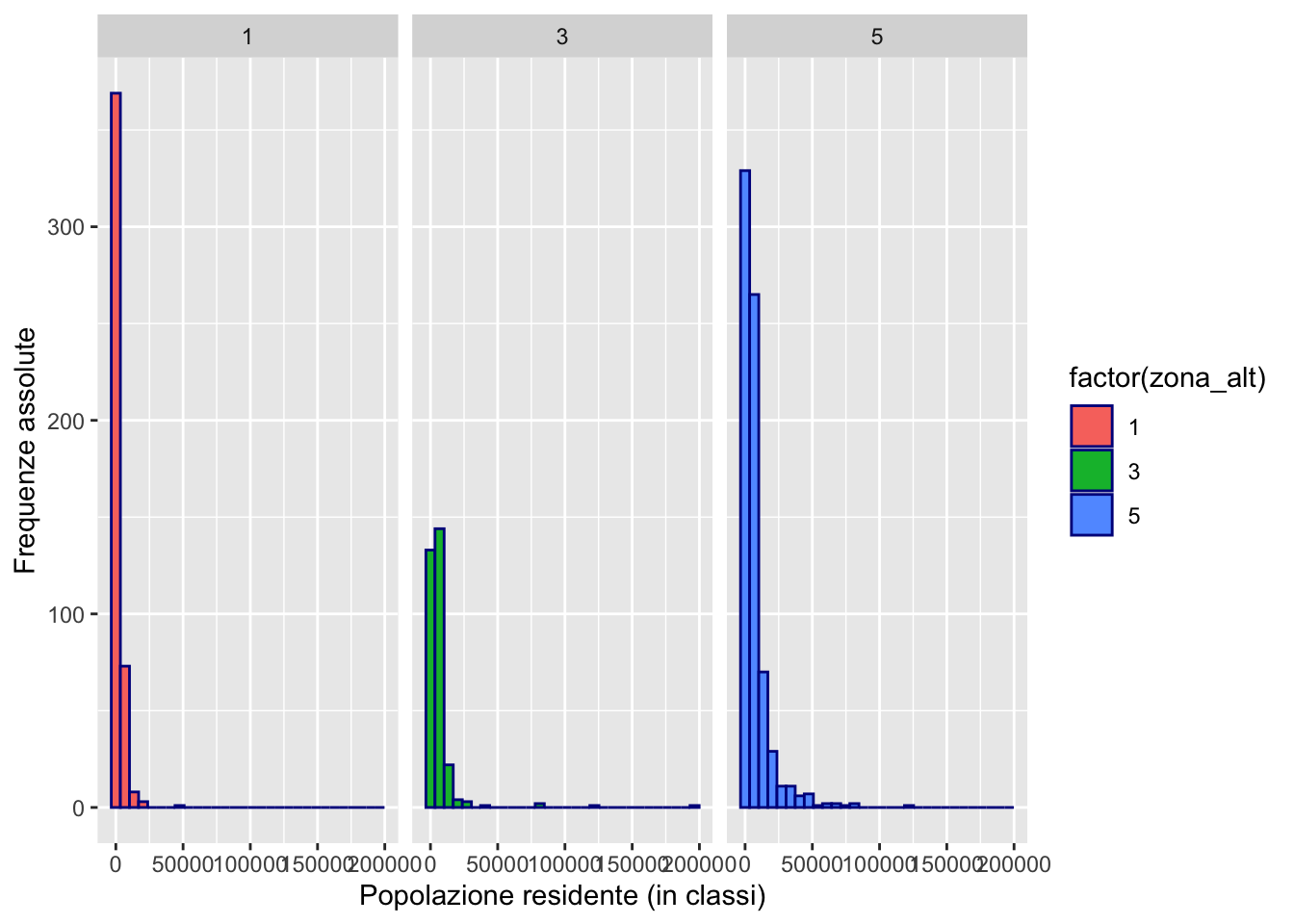
Tutte le distribuzioni sono asimmetriche con la maggior parte dei comuni collocata nella parte sinistra delle distribuzioni. In particolare la distribuzione rossa (montagna interna) è quella che ha la prima barra più elevata (classe di popolazione con valori più piccoli), mentre la distribuzione blu (pianura) è quella con la “coda a destra” più lunga, ovvero con più comuni nelle classi di popolazioni con valori maggiori. Si ricordi che è possibile calcolare le statistiche descrittive per la variabile popolazione condizionatamente a zona_alt:
datilomb %>%
group_by(zona_alt) %>%
summarise(min(pop), max(pop), mean(pop), var(pop), sd(pop)/mean(pop))# A tibble: 3 × 6
zona_alt `min(pop)` `max(pop)` `mean(pop)` `var(pop)` `sd(pop)/mean(pop)`
<int> <int> <int> <dbl> <dbl> <dbl>
1 1 32 46871 2228. 11681823. 1.53
2 3 49 196446 6605. 218002882. 2.24
3 5 59 1354196 9329. 2584152084. 5.45Il fatto che in pianura viva mediamente più gente conferma i grafici visti sopra. Inoltre, la distribuzione della poplazione in pianura presenta maggiore variabilità (CV=5.45).
5.4 Esercizi Lab 4
5.4.1 Esercizio 1
Si consideri nuovamente il dataframe dati relativo ai dati dei comuni italiani, già considerato per il Lab 3 e 4. Caricare la libreria tidyverse.
Creare la variabile
urban2come ricodificare della variabileurbanusando le categorie 1=“densamente pop”, 2=“mediamente pop”, 3=“scarsamente pop”. Costruire la distribuzione di frequenza diurban2. Quale è la moda diurban2?Rappresentare graficamente la variabile
urban2. Usare il colore marrone per il bordo e l’arancio per il riempimento.Selezionare solo i comuni nella regione Piemonte (
codreguguale a 1) creando un nuovo dataframe denominatodatipiem. Quanti comuni ci sono in Piemonte?Quanti comuni densamente popolati ci sono in Piemonte? Quali sono?
Considerando i dati piemontesi, si voglia ora studiare l’altitudine sul livello del mare (
alt). Quale è l’altitudine maggiore? A quale comune corrisponde? E quella minore? E quella media?Rappresentare graficamente l’altitudine dei comuni piemontesi usando l’istogramma. La distribuzione è simmetrica?
Modificare l’istogramma in modo da avere sottografici a seconda delle categorie di
urban2.Calcolare l’altitudine minima, media, massima, la varianza e il coefficiente di variazione condizionatamente a
urban2. Commentare.