3 Lab 2 - 08/03/2024
In questa lezione vedremo:
- come importare dati disponibili in un file di tipo comma-separated values (csv);
- come selezionare una variabile da un dataframe;
- come ricavare una distribuzione di frequenza;
- come calcolare la media e la mediana.
3.1 Importazione dei dati
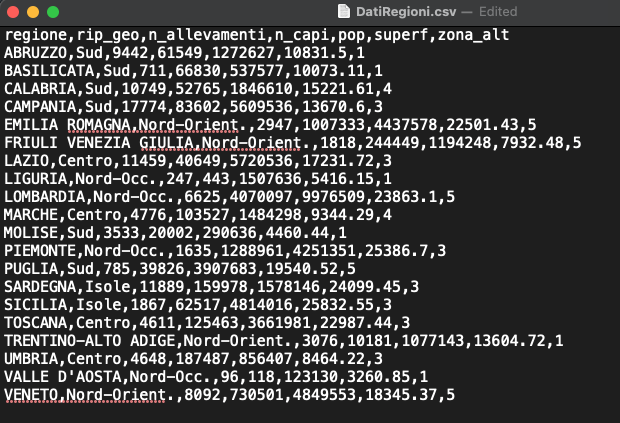
Il file DatiRegioni.csv (disponibile in Moodle nella cartella Dati) contiene i dati già discussi durante la Lezione 2, ovvero 7 variabili per le 20 regioni italiane.
Si noti che un file di tipo .csv (che normalmente viene aperto con Excel) è di fatto un file di testo che può essere aperto con un editor di testo come TextNote, TextEdit o BloccoNote. In particolare, in Figura @fig:csv vengono mostrati i dati come se aperti con un editor di testo. in questo caso la virgola risulta essere il separatore di campo. Ciò può essere diverso in altri computer poichè dipende dal sistema operativo e dalla versione (inglese/italiana) di Excel.
Ci sono 3 elementi che caratterizzano un file csv:
- header (intestazione): la prima riga del file che contiene solitamente i nomi delle variabili;
- il separatore di campo: il carattere utilizzato per separare le informazioni disponibili nel file (solitamente si utilizza il punto e virgola, la virgola, lo spazio o il tab);
- il separatore decimale: il carattere utilizzato per i decimali (solitamente si usa la virgola o il punto, dipende anche dalla versione di Excel e del sistema operativo).
Dall’anteprima del file riportata in Figura @ref(fig:csv) si nota che:
- le stringhe di testo riportate nella prima riga rappresentano i nomi delle variabili;
- “,” è il separatore di campo;
- “.” è il separatore decimale;
- ci sono due variabili categoriali (regione e rip_geo).
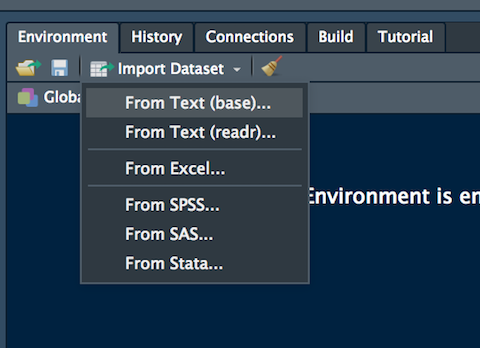
Queste informazioni devono necessariamente essere specificate in R quando si importano dei dati da un file csv. La funzione che si utilizza è read.csv(...) (si veda eventualmente ?read.csv). Per facilitare l’import dei dati, in RStudio è disponibile una funzionalità user-friendly, si veda qui per maggiori informazioni. La funzionalità “Import Dataset” è disponibile nel pannello in alto a destra (Environment) (si veda la Figura Figure 3.1). Dopo aver scelto “From text (base)” è possibile specificare tutti i settaggi del file csv nella finestra “Import Dataset”, come riportato in Figura Figure 3.2.
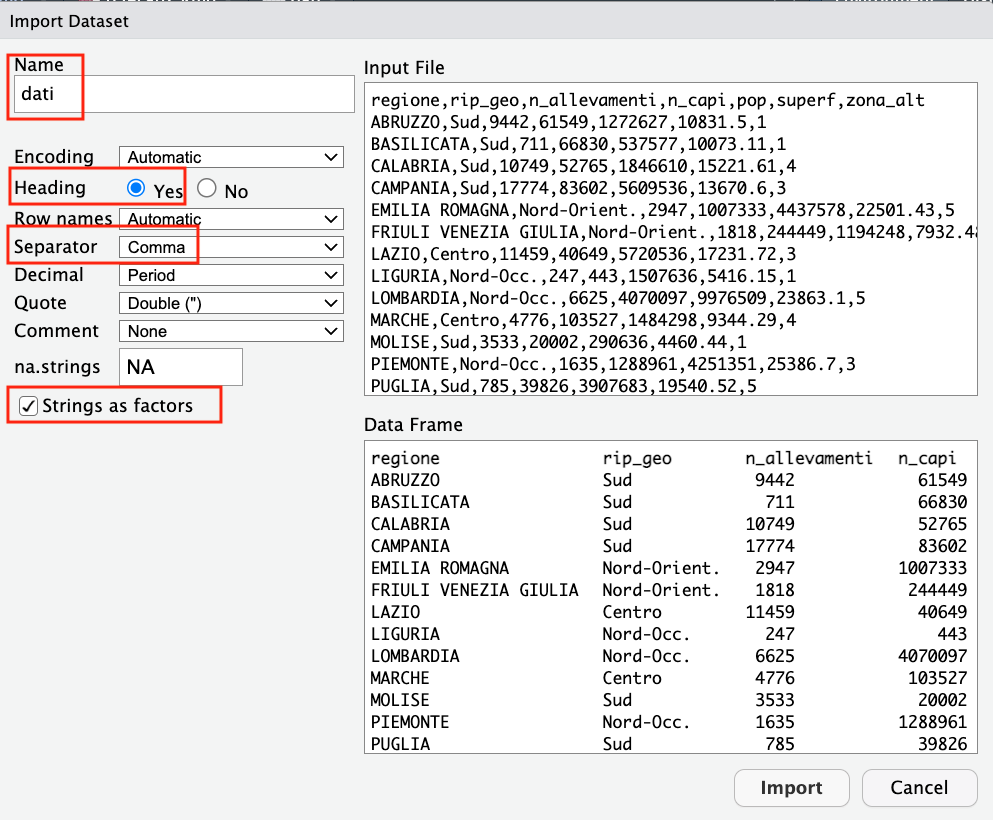
Si noti che viene anche spuntata l’opzione “Strings as factors”. Questo permette di interpretare tutte le variabili categoriali in maniera corretta (ovvero come “fattori” secondo le regole di R). Dopo aver cliccato su Import si verificano tre cose:
- un oggetto di nome
dativiene creato nell’ambiente di lavoro (si veda il pannello in alto a destra). E’ un nuovo oggetto di tipo dataframe, - viene aperta nel pannello in alto a sinistra una nuova tab che riporta la preview dei dati,
- nella Console (pannello in basso a sinistra) viene riportato il codice utilizzato, tramite la funzionalità user-friendly, per importare i dati. Esso è riportato qui di seguito:
dati <- read.csv("./data/DatiRegioni.csv", stringsAsFactors = T)dove ovviamente il percorso riportato tra virgolette dipende dalla posizione del file nel proprio PC. Si consiglia di copiare questa linea di codice nello script in uso. Ciò permetterà successivamente di importare i dati usando direttamente il codice (in modo più veloce) e non la funzionalità Import Dataset di RStudio.
L’oggetto dati è un oggetto di tipo data.frame:
class(dati)[1] "data.frame"I data frame sono matrici di dati le cui righe si riferiscono ai soggetti (in questo caso alle regioni) e le colonne alle variabili.
Utilizzando la funzione str si ottengono informazioni circa la tipologia delle variabili incluse nel data frame:
str(dati)'data.frame': 20 obs. of 7 variables:
$ regione : Factor w/ 20 levels "ABRUZZO","BASILICATA",..: 1 2 3 4 5 6 7 8 9 10 ...
$ rip_geo : Factor w/ 5 levels "Centro","Isole",..: 5 5 5 5 4 4 1 3 3 1 ...
$ n_allevamenti: int 9442 711 10749 17774 2947 1818 11459 247 6625 4776 ...
$ n_capi : int 61549 66830 52765 83602 1007333 244449 40649 443 4070097 103527 ...
$ pop : int 1272627 537577 1846610 5609536 4437578 1194248 5720536 1507636 9976509 1484298 ...
$ superf : num 10832 10073 15222 13671 22501 ...
$ zona_alt : int 1 1 4 3 5 5 3 1 5 4 ...Si noti che regione e rip_geo sono interpretate come factor, ovvero variabili categoriali, mentre tutte le altre variabili come caratteri quantitativi. Attenzione a zona_alt: viene interpretato come variabile numerica ma noi in realtà sappiamo che 1=Montagna interna; 2=Montagna litoranea; 3=Collina interna; 4=Collina litoranea; 5=Pianura. Sarà in questo caso necessario fare una ricodifica.
Utilizzando le funzioni head e tail è possibile ottenere visualizzare la parte superiore e inferiore del data frame:
head(dati) #prime 6 righe in alto regione rip_geo n_allevamenti n_capi pop superf
1 ABRUZZO Sud 9442 61549 1272627 10831.50
2 BASILICATA Sud 711 66830 537577 10073.11
3 CALABRIA Sud 10749 52765 1846610 15221.61
4 CAMPANIA Sud 17774 83602 5609536 13670.60
5 EMILIA ROMAGNA Nord-Orient. 2947 1007333 4437578 22501.43
6 FRIULI VENEZIA GIULIA Nord-Orient. 1818 244449 1194248 7932.48
zona_alt
1 1
2 1
3 4
4 3
5 5
6 5tail(dati) #ultime 6 righe in basso regione rip_geo n_allevamenti n_capi pop superf
15 SICILIA Isole 1867 62517 4814016 25832.55
16 TOSCANA Centro 4611 125463 3661981 22987.44
17 TRENTINO-ALTO ADIGE Nord-Orient. 3076 10181 1077143 13604.72
18 UMBRIA Centro 4648 187487 856407 8464.22
19 VALLE D'AOSTA Nord-Occ. 96 118 123130 3260.85
20 VENETO Nord-Orient. 8092 730501 4849553 18345.37
zona_alt
15 3
16 3
17 1
18 3
19 1
20 5Per ottenere informazioni circa le dimensioni del data frame (numero di righe e colonne) si possono utilizzare le seguenti funzioni alternative:
nrow(dati) #n. di righe[1] 20ncol(dati) #n. di colonne[1] 73.2 Analisi esplorative su singole variabili
Nel dataframe ogni colonna contiene una variabile, ovvero un vettore i cui valori possono essere estratti usando l’operatore $. Ad esempio,
dati$regione [1] ABRUZZO BASILICATA CALABRIA
[4] CAMPANIA EMILIA ROMAGNA FRIULI VENEZIA GIULIA
[7] LAZIO LIGURIA LOMBARDIA
[10] MARCHE MOLISE PIEMONTE
[13] PUGLIA SARDEGNA SICILIA
[16] TOSCANA TRENTINO-ALTO ADIGE UMBRIA
[19] VALLE D'AOSTA VENETO
20 Levels: ABRUZZO BASILICATA CALABRIA CAMPANIA ... VENETOrestuisce il vettore con tutti i nomi di regione.
Per calcolare la distribuzione di frequenza della variabile rip_geo si utilzza la funzione table:
table(dati$rip_geo)
Centro Isole Nord-Occ. Nord-Orient. Sud
4 2 4 4 6 Si ottiene un output che riporta le 5 categorie della variabile e le corrispondente frequenze assoluta \(n_i\). La moda (si veda la teoria in MAD2324_Lez3.pdf) è la categoria che si presenta maggiormente (con la frequenza maggiore): in questo caso la modalità SUD rappresenta la moda avendo essa il maggior numero di regioni (6). E’ anche possibile calcolare le frequenze relative \(f_i=\frac{n_i}{n}\) andando a dividere le frequenze assolute per il numero totale di unità statistiche (\(n=20\)). Quest’ultime corrispondono al numero di righe del dataframe e si possono ricavare con la funzione nrow:
nrow(dati)[1] 20# distr. di frequenza con frequenze relative
table(dati$rip_geo)/nrow(dati)
Centro Isole Nord-Occ. Nord-Orient. Sud
0.2 0.1 0.2 0.2 0.3 # distr. di frequenza con frequenze percentuali
table(dati$rip_geo)/nrow(dati)*100
Centro Isole Nord-Occ. Nord-Orient. Sud
20 10 20 20 30 Il 30% delle regioni italiane si trova al Sud.
Si noti che ha senso calcolare la distribuzione di frequenza quando il numero di modalità univoche è ridotte (5 nel caso precedente). Provando a calcolare la distribuzione di frequenza per la variabile n_allevamenti si otterrebbe quanto segue:
table(dati$n_allevamenti)
96 247 711 785 1635 1818 1867 2947 3076 3533 4611 4648 4776
1 1 1 1 1 1 1 1 1 1 1 1 1
6625 8092 9442 10749 11459 11889 17774
1 1 1 1 1 1 1 E’ evidente che ogni modalità (numerica) si presenta solamente una volta (tutte le \(n_i\) sono pari a 1) e quindi la distribuzione di frequenza non ha effettuato la sintesi sperata. In tal caso è necessario creare delle classi di valori prima di calcolare la distribuzione di frequenza.
Si consideri ora la variabile n_allevamenti. Per il calcolo del numero totale di allevamenti in Italia si utilizza la funzione somma:
sum(dati$n_allevamenti)[1] 106780Volendo equidistribuzione (in maniera del tutto ipotetica) il numero di allevamenti tra le 20 regioni si otterrebbe il seguente valore:
sum(dati$n_allevamenti) / nrow(dati) [1] 5339che di fatto corrisponde con la media aritmetica del carattere:
mean(dati$n_allevamenti)[1] 5339La media aritmetica è infatti quell’indice che mantiene inalterato il totale del fenomeno (106780 allevamenti) qualora il valore di ogni regione venisse sostituito con la media.
Un altro indice di interesse è la mediana (si veda la teoria in MAD2324_Lez3.pdf) che può essere calcolata con la funzione median:
median(dati$n_allevamenti)[1] 4072Ciò ci dice che almeno il 50% delle regioni (in particolare 10 regioni su 20) ha un numero di allevamenti minore o uguale a 4072. Analogamente almeno il 50% delle regioni (in particolare 10 regioni su 20) ha un numero di allevamenti maggiore o uguale a 4072.
3.3 Esercizi Lab 2
3.3.1 Esercizio 1
Si considerino nuovamente i dati disponibili nel file DatiRegioni.csv. Calcolare quanto segue:
- il totale della popolazione residente in Italia.
- la superficie totale dell’Italia.
- Il numero medio e mediano di abitanti per regione. Interpretare i valori.
- La superficie media e mediana per regione. Interpretare i valori.
3.3.2 Esercizio 2
Si consideri il file Excel Classificazioni statistiche-e-dimensione-dei-comuni_31_12_2023.xlsx fornito da Istat. Si noti che è composta da tre fogli di lavoro (il primo contiene i dati, il secondo la loro descrizione).
Effettuare le seguenti operazioni:
- aprire il file con Excel.
- Nel primo foglio di lavoro (Comuni 31-12-2023) cambiare il nome delle colonne usando i seguenti nomi:
codreg,codcom,nomecom,sup,pop,zona_alt,alt,lito,isol,cost,urban. - Togliere il separatore delle migliaia utilizzato per alcune delle variabili numeriche.
- Eliminare gli altri due fogli di lavoro e salvare il file in formato csv. Chiamare il file
DatiCom.csv. - Importare il file in RStudio creando un oggetto di nome
daticom(ignorare gli eventuali messaggi di warning dovuti ai comuni con nome accentato). Quante righe e quante colonne ha il dataframe? - Controllare la natura delle variabili nel dataframe
daticom(in base alla loro conoscenza preliminare). - Ricavare la distribuzione di frequenza della variabile
codreg(eventualmente vedere qui per i nomi e codici delle regioni). Calcolare, se possibile, la moda, la media e la mediana. - Ricavare la distribuzione di frequenza della variabile
zona_alt(anche includendo le frequenze percentuali). Calcolare, se possibile, la moda, la media e la mediana. - Ricavare la distribuzione di frequenza della variabile
alt. Calcolare, se possibile, la moda, la media e la mediana.