6 Lab 5 - 05/04/2024

In questa lezione vedremo:

come rappresentare graficamente una variabile quantitativa utilizzando il boxplot,
come fare il reshape di un dataset da formato wide a formato long.

Verrà utilizzato un nuovo dataset riguardante il consumo di suolo nelle province italiane reso disponibile da ISPRA (si veda qui per maggiori dettagli). Come descritto nel report ISPRA, “il consumo di suolo è un processo associato alla perdita di una risorsa ambientale fondamentale, limitata e non rinnovabile, dovuta all’occupazione di una superficie originariamente agricola, naturale o seminaturale con una copertura ufficiale”.

I dati sono disponibili nel file consumosuolo.csv disponibile nella cartella Dati della pagina Moodle del corso. Li importiamo come già descritto in Section 3.1 andando a creare un oggetto di nome suolo:

suolo = read.csv("./data/consumosuolo.csv")

Come prima cosa è necessario caricare il pacchetto tidyverse (come descritto in Section 4.2):

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.0
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.2     ✔ tidyr     1.3.0
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Con il comando glimpse andiamo a visionare le caratteristiche delle variabili contenute nel dataframe appena creato:

glimpse(suolo)

Rows: 107
Columns: 12
$ Provincia <chr> "Torino", "Vercelli", "Novara", "Cuneo", "Asti", "Alessandri…
$ Regione   <chr> "Piemonte", "Piemonte", "Piemonte", "Piemonte", "Piemonte", …
$ perc2006  <dbl> 8.15, 4.70, 10.33, 4.98, 6.93, 6.58, 2.08, 6.23, 6.50, 7.86,…
$ perc2012  <dbl> 8.36, 4.87, 10.72, 5.17, 7.12, 6.89, 2.10, 6.30, 6.61, 7.91,…
$ perc2015  <dbl> 8.40, 4.89, 10.76, 5.19, 7.13, 6.92, 2.12, 6.33, 6.63, 7.94,…
$ perc2016  <dbl> 8.41, 4.89, 10.79, 5.20, 7.14, 6.94, 2.13, 6.33, 6.64, 7.94,…
$ perc2017  <dbl> 8.44, 4.92, 10.82, 5.22, 7.17, 6.97, 2.13, 6.34, 6.64, 7.94,…
$ perc2018  <dbl> 8.46, 4.93, 10.85, 5.24, 7.18, 6.99, 2.14, 6.34, 6.65, 7.95,…
$ perc2019  <dbl> 8.48, 4.93, 10.88, 5.25, 7.20, 7.01, 2.14, 6.35, 6.66, 7.95,…
$ perc2020  <dbl> 8.51, 4.93, 10.96, 5.27, 7.21, 7.04, 2.14, 6.35, 6.67, 7.96,…
$ perc2021  <dbl> 8.54, 4.95, 11.07, 5.29, 7.24, 7.07, 2.15, 6.35, 6.68, 7.96,…
$ perc2022  <dbl> 8.56, 4.97, 11.14, 5.31, 7.25, 7.09, 2.15, 6.36, 6.69, 7.97,…

Sono presenti due variabili qualitative sconnesse (Provincia e Regione) e 10 variabili quantitative relative alla percentuale di suolo consumato (sul totale della superficie di ogni provincia) per ogni provincia per alcuni anni (2006, 2012, 2015-2022). Il dataset ha 107 righe come il numero di province in Italia.

Il seguente codice permette di ottenere la distribuzione di frequenza della variabile Regione, ovvero di conteggiare quante volte ogni regione si ripete nel dataframe, dandoci quindi l’informazione di quante province ci sono in ogni regione:

suolo %>% 
  count(Regione)

                 Regione  n
1                Abruzzo  4
2             Basilicata  2
3               Calabria  5
4               Campania  5
5         Emilia-Romagna  9
6  Friuli Venezia Giulia  4
7                  Lazio  5
8                Liguria  4
9              Lombardia 12
10                Marche  5
11                Molise  2
12              Piemonte  8
13                Puglia  6
14              Sardegna  5
15               Sicilia  9
16               Toscana 10
17   Trentino-Alto Adige  2
18                Umbria  2
19         Valle d'Aosta  1
20                Veneto  7

La regione modale è la Lombardia perchè è quella che si presenta maggiormente (ha infatti 12 province). La regione Valle d’Aosta ha una sola provincia e quindi la sua frequenza assoluta è pari a 1.

6.1 Quartili e boxplot

Si consideri ora la variabile perc2006, ovvero la percentuale di suolo consumato nell’anno 2006. Andiamo a rappresentare questa distribuzione (107 valori) utilizzando un istogramma (si veda Section 5.3):

suolo %>% 
  ggplot() +
  geom_histogram(aes(perc2006), col = "blue")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.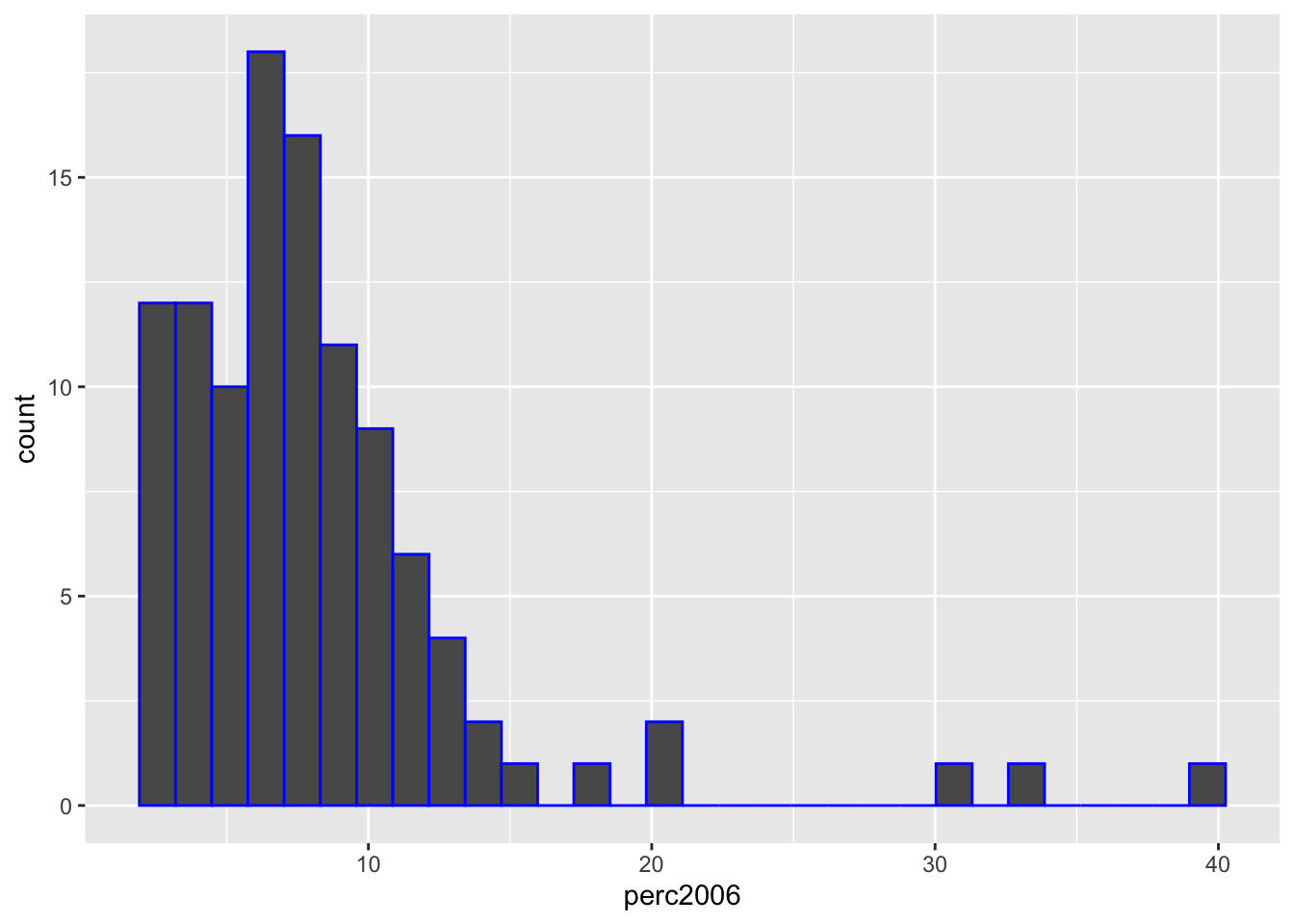

L’asse delle y riporta il conteggio del numero di province che hanno un valore di percentuale di suolo consumato in una certa classe di valori (le classi sono sull’asse delle x). La maggior parte delle province sono nella parte sinistra del grafico ma si notano valori isolati nella parte destra dati da province che nel 2006 hanno valori particolarmente alti di suolo consumato (la distribuzione è asimmetrica). Utilizzando il verbo filter (introdotto in Section 5.2) è possibile selezionare le province con una percentuale maggiore di 30:

suolo %>% 
  filter(perc2006 > 30)

              Provincia   Regione perc2006 perc2012 perc2015 perc2016 perc2017
1                Milano Lombardia    30.27    31.02    31.36    31.41    31.47
2                Napoli  Campania    33.11    33.71    33.92    34.01    34.13
3 Monza e della Brianza Lombardia    39.14    40.11    40.32    40.33    40.41
  perc2018 perc2019 perc2020 perc2021 perc2022
1    31.52    31.56    31.62    31.69    31.81
2    34.24    34.35    34.44    34.62    34.71
3    40.44    40.50    40.58    40.60    40.72

Analogamente è possibile trovare quale è la provincia con la minor percentuale di suolo consumato nel 2006:

suolo %>% 
  filter(perc2006 == min(perc2006))

  Provincia       Regione perc2006 perc2012 perc2015 perc2016 perc2017 perc2018
1     Aosta Valle d'Aosta     2.08      2.1     2.12     2.13     2.13     2.14
  perc2019 perc2020 perc2021 perc2022
1     2.14     2.14     2.15     2.15

Andiamo ora a calcolare i tre quartili \(Q_1\) (primo quartile), \(Q_2\) (mediana) e \(Q_3\) (terzo quartile) per la variabile perc2006:

suolo %>% 
  summarise(Q1 = quantile(perc2006,0.25),
            Q2 = median(perc2006),
            Q3 = quantile(perc2006, 0.75))

    Q1   Q2    Q3
1 5.03 7.12 9.645

Si commentano come segue i tre valori:

il 25% (circa) delle province ha una percentuale di suolo consumato nel 2006 \(\leq\) 5.03 (\(Q_1\)); il 75% (circa) delle province ha una percentuale di suolo consumato nel 2006 \(\geq\) 5.03
il 50% (circa) delle province ha una percentuale di suolo consumato nel 2006 \(\leq\) 7.12 (mediana); il 50% (circa) delle province ha una percentuale di suolo consumato nel 2006 \(\geq\) 7.12
il 75% (circa) delle province ha una percentuale di suolo consumato nel 2006 \(\leq\) 9.645 (\(Q_3\)); il 25% (circa) delle province ha una percentuale di suolo consumato nel 2006 \(\geq\) 9.645

E’ possibile anche calcolare la differenza interquartile \(IQR=Q_3-Q_1\):

suolo %>% 
  summarise(Q1 = quantile(perc2006,0.25),
            Q2 = median(perc2006),
            Q3 = quantile(perc2006, 0.75)) %>% 
  mutate(IQR = Q3-Q1)

    Q1   Q2    Q3   IQR
1 5.03 7.12 9.645 4.615

Si ricordi che l’\(IQR\) è un indice di variabilità: più alto è, maggiore la variabilità (utile soprattutto in termini comparativi).

I quartili si utilizzano per la costruzione del boxplot che può essere ottenuto utilizzando la geometria geom_boxplot:

suolo %>% 
  ggplot() +
  geom_boxplot(aes(perc2006))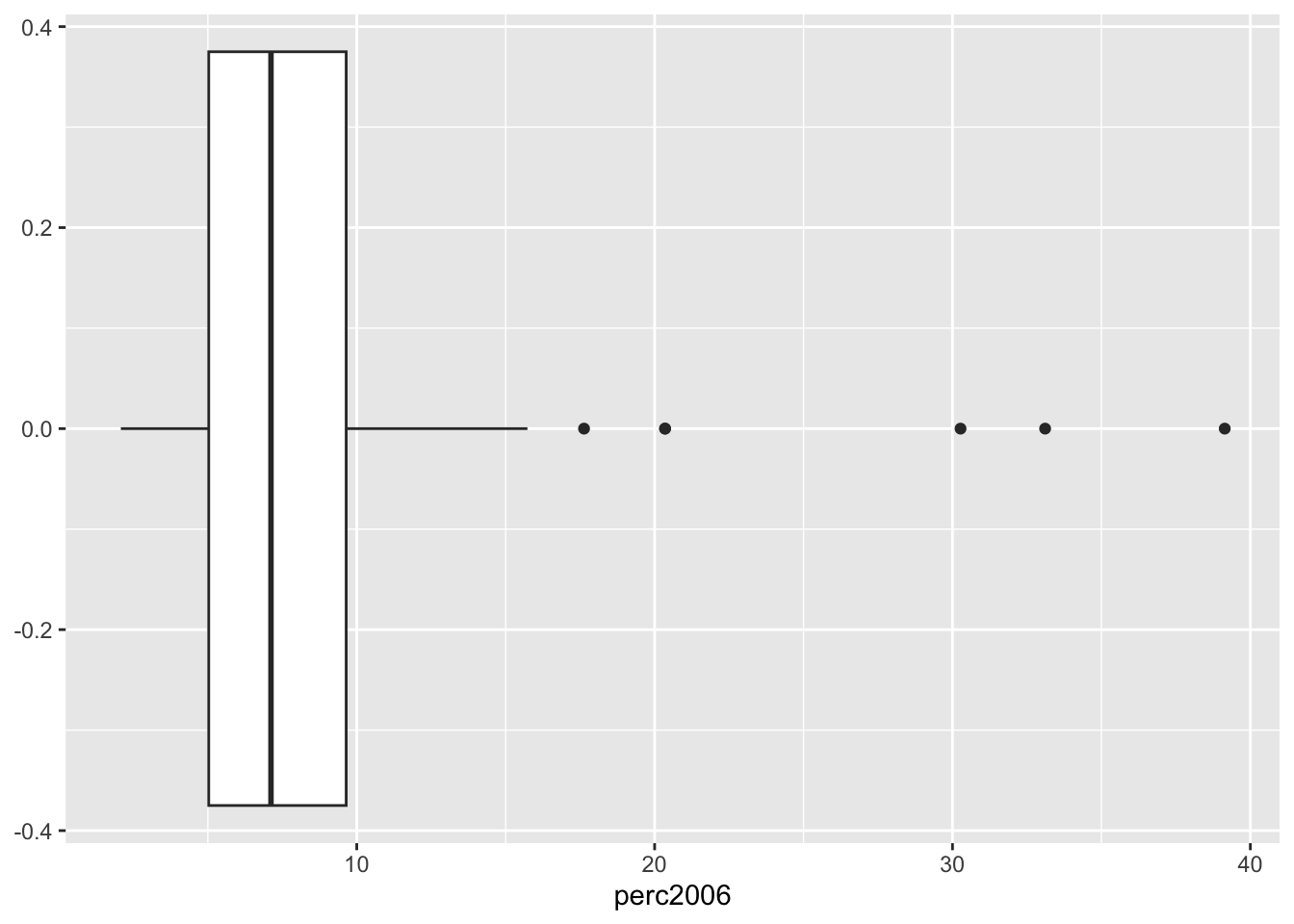

Sull’asse delle x si riportano i valori della variabile perc2006 (non si guardino i valori sull’asse delle y che non hanno alcun significato). Si ricordi che la scatola contiene il 50% circa delle osservazioni centrali della distribuzione. Sulla parte destra (valori elevati di perc2006) si osservano 4 valori estremi, ovvero 4 province che hanno un valore particolarmente elevato di suolo consumato.

6.2 Da formato wide a long: piccolo esempio

Si consideri il seguente dataset fittizio relativo alle concentrazioni di PM10 (valori nelle celle) per 3 province (X, Y e Z) e quattro giorni (da giorno1 a giorno4):

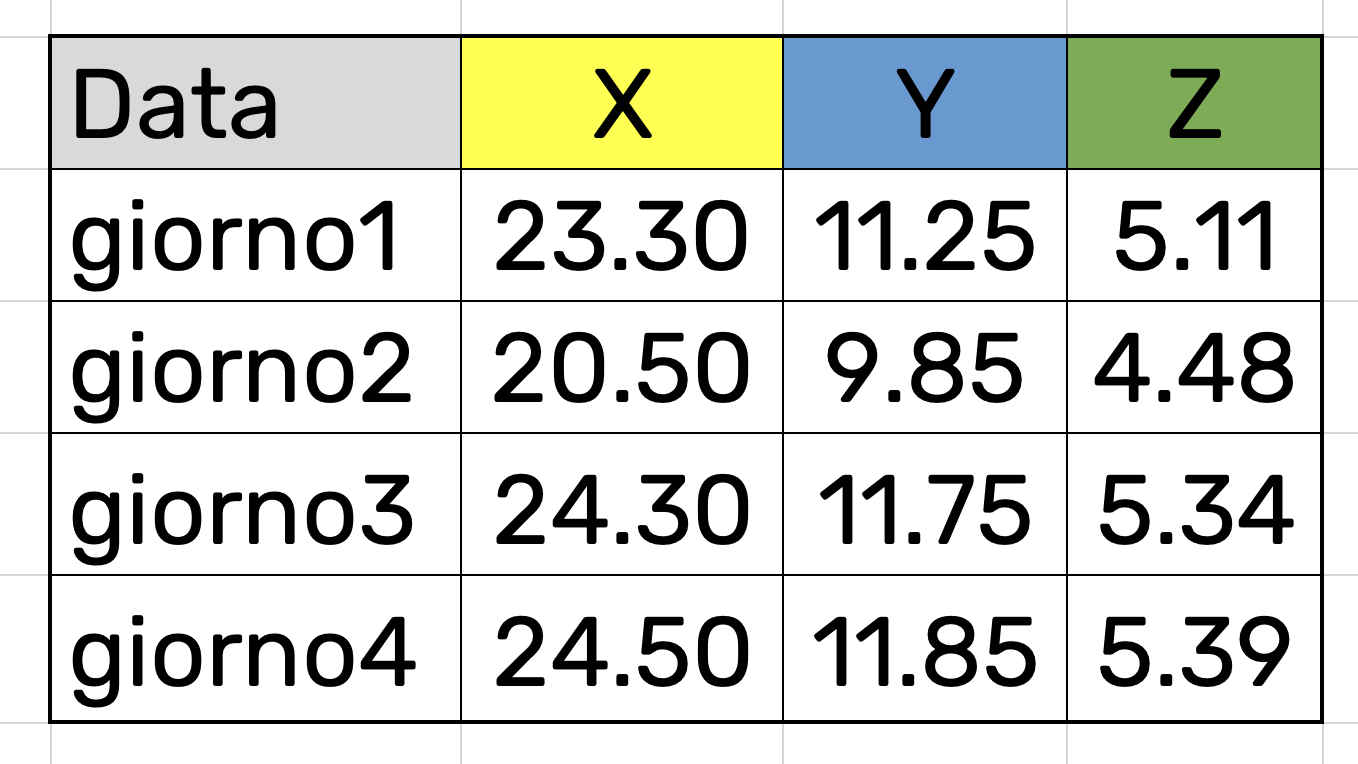
Esempio di dataset in formato wide

Il numero di righe è dato dal numero di giorni (4) e il numero di colonne dal numero di province (3) più uno (per la data). Si noti che le colonne X, Y e Z contengono 12 valori. Facendo il reshape andremo a mettere questi 12 valori in un’unica colonna (denominata PM10), andando poi a creare una nuova colonna (denominata Prov) che vada a specificare la provincia a cui si riferiscono i valori:

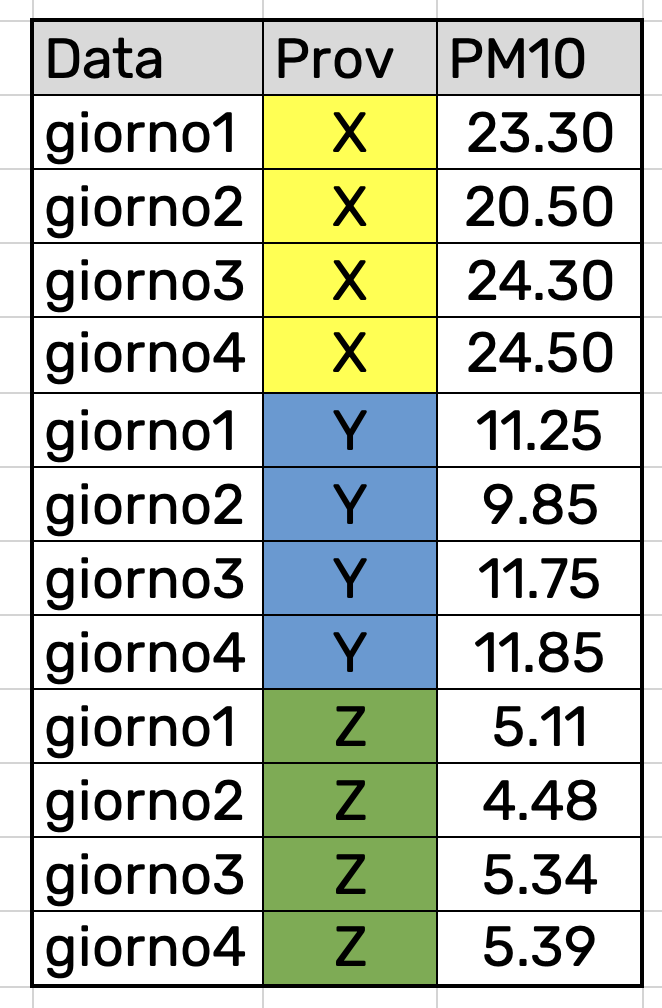
Esempio di dataset in formato long

Ovviamente le 4 date vanno ripetute: in questo modo il numero di righe sarà dato dal prodotto tra il numero di giorni e il numero di province. Il numero di colonne invece sarà sempre 3 (Data, Prov, PM10) indipendentemente dal numero di province che si considerano.

6.3 Da formato wide a long per `suolo`

Per fare il reshape del dataframe suolo da wide a long si utilizza la funzione pivot_longer andando poi a creare un nuovo dataframe denominato suololong:

suololong = suolo %>% 
  pivot_longer(perc2006:perc2022,
               names_to = "anno",
               values_to = "perc")
dim(suololong)

[1] 1070    4

glimpse(suololong)

Rows: 1,070
Columns: 4
$ Provincia <chr> "Torino", "Torino", "Torino", "Torino", "Torino", "Torino", …
$ Regione   <chr> "Piemonte", "Piemonte", "Piemonte", "Piemonte", "Piemonte", …
$ anno      <chr> "perc2006", "perc2012", "perc2015", "perc2016", "perc2017", …
$ perc      <dbl> 8.15, 8.36, 8.40, 8.41, 8.44, 8.46, 8.48, 8.51, 8.54, 8.56, …

Il codice perc2006:perc2022 specifica che le colonne che devono essere modificate sono quelle DA perc2006 A perc2022 (le colonne Provincia e Regione verranno aggiustate - ovvero ripetute - di conseguenza). Le opzione names_to e values_to ci permettono di definire i nomi delle due nuove colonne che verranno create, una per l’anno e una per i valori percentuali (ogni nome è valido basta usare le virgolette).

Vediamo che suololong ha 1070 righe (107 province ripetute per 10 anni) e 4 colonne. Avendo più righe rispetto al dataframe suolo il formato dei dati è ora di tipo long.

Si noti che la colonna anno è di tipo chr (carattere) in quanto ogni anno è preceduto dal prefisso perc. Per poterlo rimuovere è possibile utilizzare la funzione str_replace (una sorta di “trova e sostituisci”) all’interno del verbo mutate (si veda Section 4.4.2):

suololong = suololong %>% 
  mutate(anno = str_replace(anno, "perc", ""))
glimpse(suololong)

Rows: 1,070
Columns: 4
$ Provincia <chr> "Torino", "Torino", "Torino", "Torino", "Torino", "Torino", …
$ Regione   <chr> "Piemonte", "Piemonte", "Piemonte", "Piemonte", "Piemonte", …
$ anno      <chr> "2006", "2012", "2015", "2016", "2017", "2018", "2019", "202…
$ perc      <dbl> 8.15, 8.36, 8.40, 8.41, 8.44, 8.46, 8.48, 8.51, 8.54, 8.56, …

La colonna anno è stata modificata ma è ancora di tipo chr.

6.4 Boxplot quando i dati sono in formato long

Il formato long ci permette di rappresentare in maniera agevole tanti boxplot affiancati. Ad esempio è possibile avere un boxplot per ogni anno come segue:

suololong %>% 
  ggplot() +
  geom_boxplot(aes(anno, perc), fill="pink")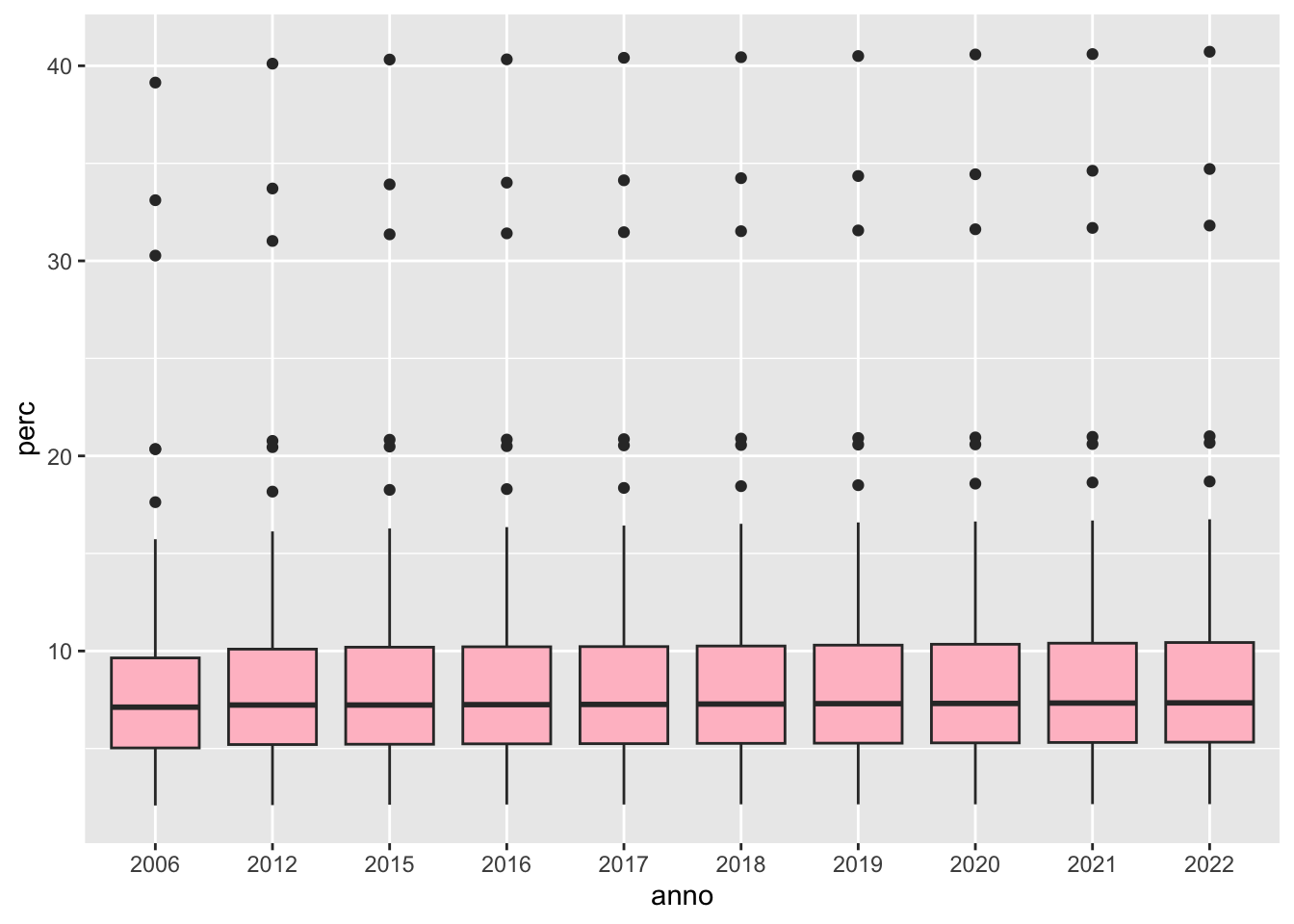

Ogni boxplot annuale è costruito utilizzando 107 valori riferiti alla variabile perc2006 per un particolare anno. Si può notare che nel corso degli anni la mediana di perc è praticamente rimasta invariata, così come le scatole dei boxplot. Si nota un ridotto incremento dei valori percentuali per quanto riguarda gli outlier (come ad esempio la provincia di Monza-Brianza):

suololong %>% 
  filter(Provincia == "Monza e della Brianza")

# A tibble: 10 × 4
   Provincia             Regione   anno   perc
   <chr>                 <chr>     <chr> <dbl>
 1 Monza e della Brianza Lombardia 2006   39.1
 2 Monza e della Brianza Lombardia 2012   40.1
 3 Monza e della Brianza Lombardia 2015   40.3
 4 Monza e della Brianza Lombardia 2016   40.3
 5 Monza e della Brianza Lombardia 2017   40.4
 6 Monza e della Brianza Lombardia 2018   40.4
 7 Monza e della Brianza Lombardia 2019   40.5
 8 Monza e della Brianza Lombardia 2020   40.6
 9 Monza e della Brianza Lombardia 2021   40.6
10 Monza e della Brianza Lombardia 2022   40.7

Volendo calcolare le 10 mediane annuali della percentuale di suolo utilizzare si utilizza summarise insieme a group_by (Section 4.4.5):

suololong %>% 
  group_by(anno) %>% 
  summarise(median(perc))

# A tibble: 10 × 2
   anno  `median(perc)`
   <chr>          <dbl>
 1 2006            7.12
 2 2012            7.23
 3 2015            7.23
 4 2016            7.25
 5 2017            7.26
 6 2018            7.28
 7 2019            7.3 
 8 2020            7.31
 9 2021            7.33
10 2022            7.34

Si nota un minimo incremento della mediana dal 2006 al 2022 (impercettibile dal grafico precedente).

Anzichè ragionare per anno si può ragionare per regione, andando a studiare la distribuzione di perc nelle regioni:

suololong %>% 
  ggplot() +
  geom_boxplot(aes(Regione, perc)) +
  theme(axis.text.x = element_text(angle = 45, hjust=1)) # per girare le etichette dell'asse delle x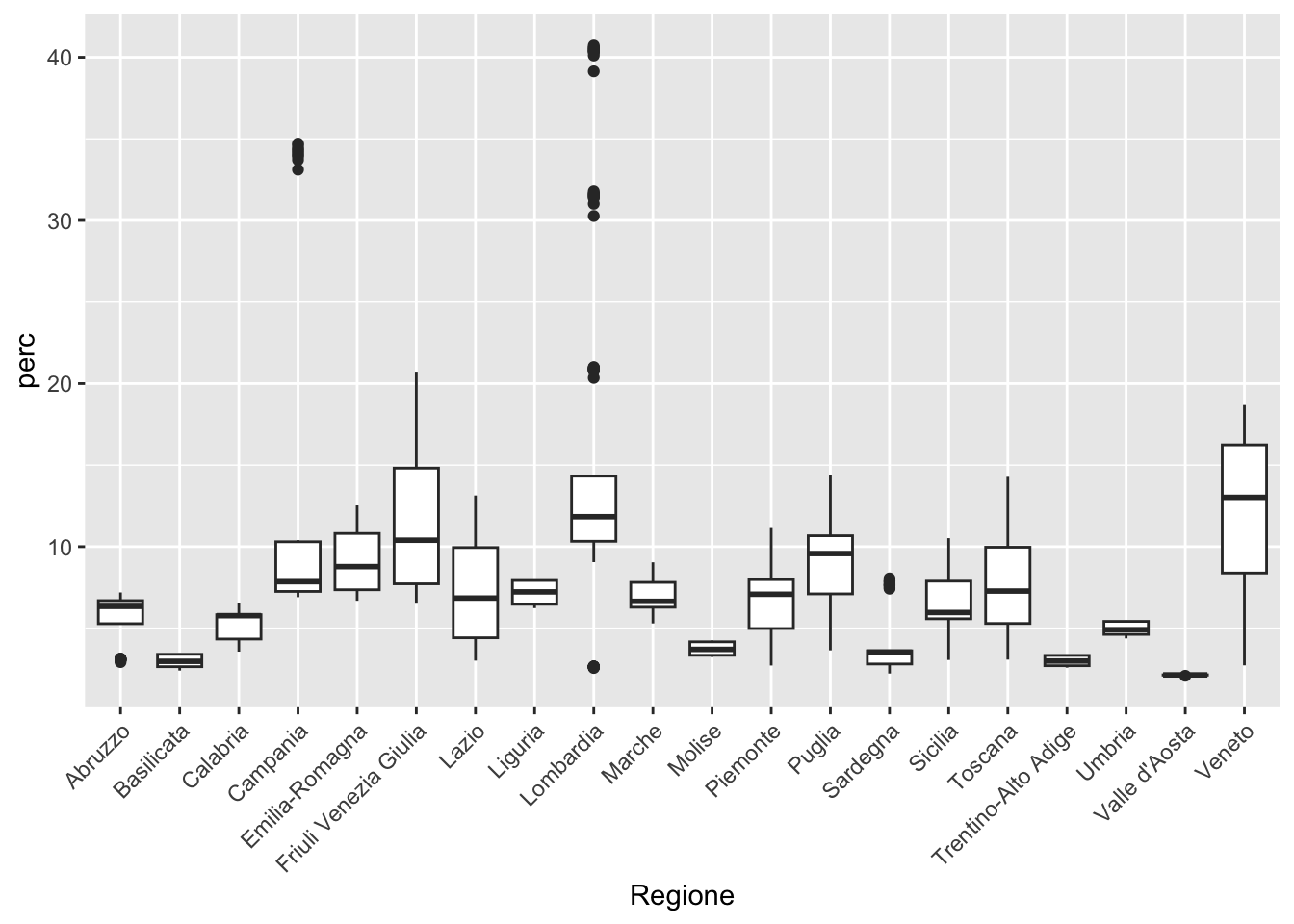

In questo caso ogni boxplot si riferisce ad una regione ed è realizzato utilizzando i dati riferiti a tutte le province della regione stessa e a tutti i 10 anni disponibili. Si nota la diversità che esiste, in termini di consumo di suolo, tra le diverse regioni, con il Veneto che presenta la mediana più elevata, seguita dalla Lombardia. Quest’ultima, insieme alla Campania, presenta valori estremi nella parte alta della distribuzione (valori elevati di perc).

6.5 Come rappresentare graficamente una serie storica

E’ possibile rappresentare graficamente l’evoluzione temporale di un fenomento tramite una linea. Servirà quindi la geometria geom_line per creare una linea che collega i valori di perc per gli anni disponibili (che andranno sull’asse delle x):

suololong %>% 
  ggplot() +
  geom_line(aes(anno, perc,
                group = Provincia))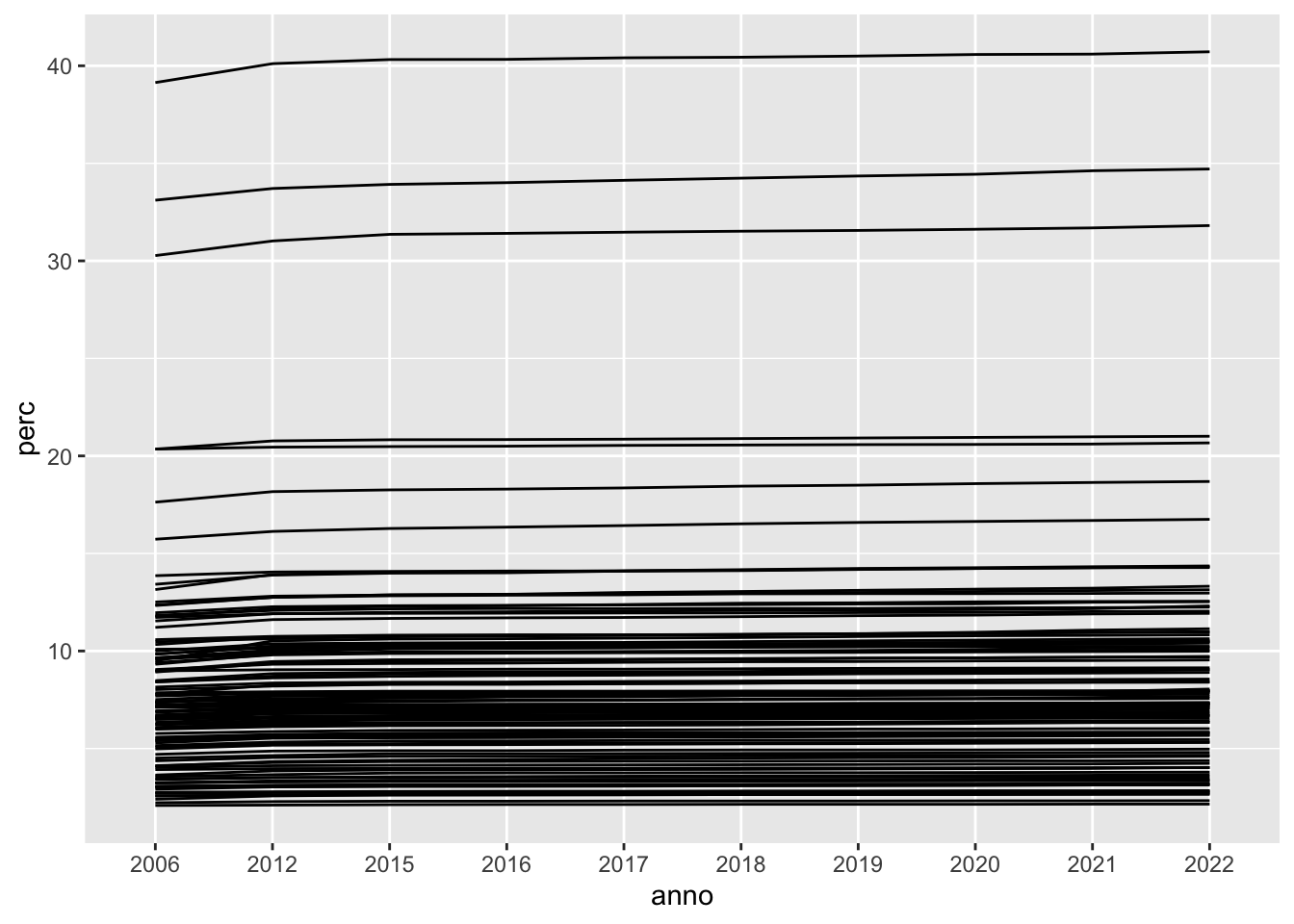

L’opzione group permette di specificare quali sono i valori da unire anno per anno. Con la specifica group = Provincia si vanno ad unire i valori di perc di ogni provincia andando così ad ottenere 107 linee separate che si muovono nel tempo. Siccome è difficile leggere il grafico si decide di selezionare solamente una regione, la Lombardia:

suololong %>% 
  filter(Regione == "Lombardia") %>% 
  ggplot() +
  geom_line(aes(anno, perc,
                group = Provincia,
                col = Provincia))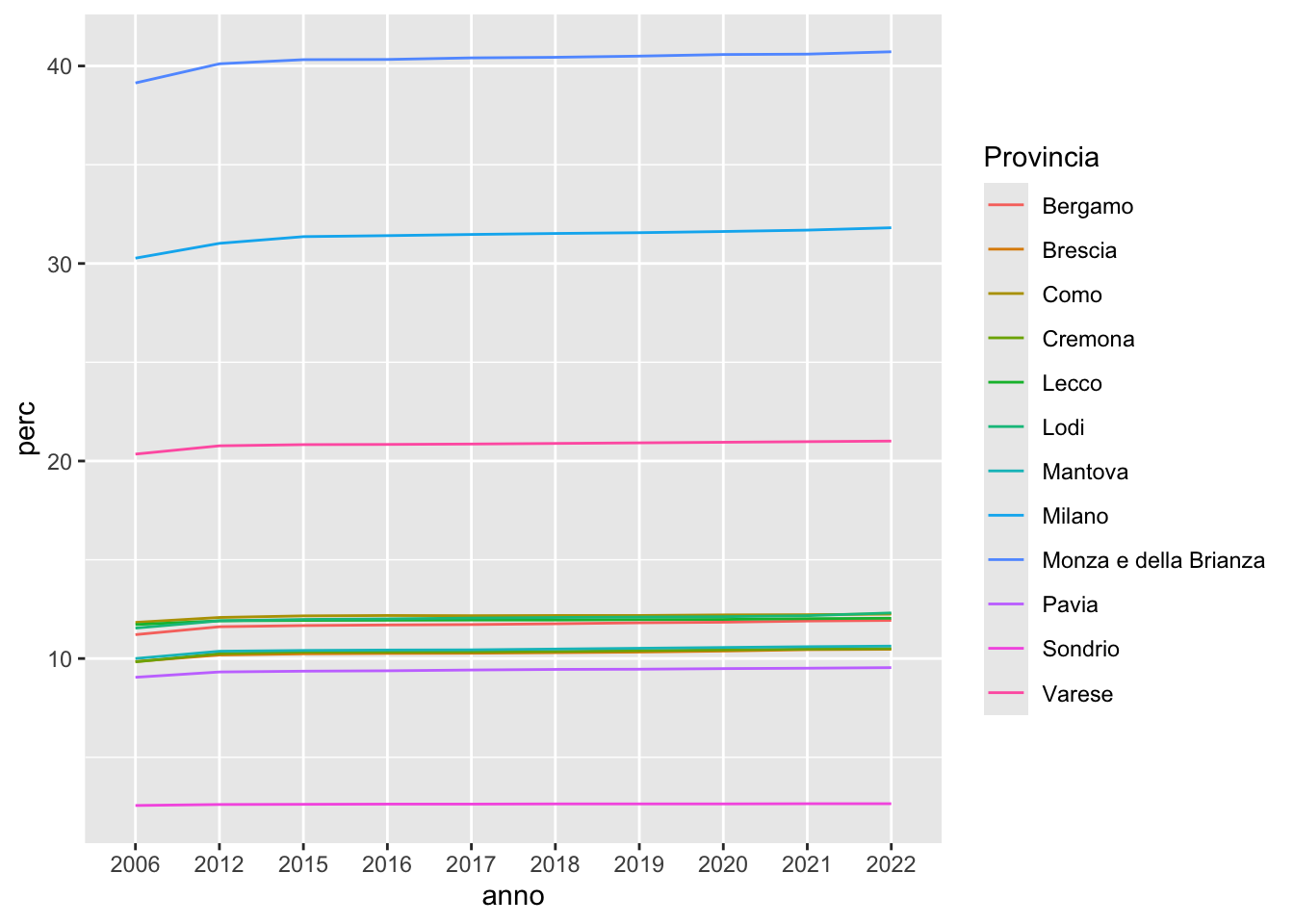

In questo caso si ottengono 12 linee (colorate secondo le modalità di Provincia). Nel tempo i valori crescono leggermente (soprattutto dal 2006 al 2012) per poi rimanere pressochè costanti. La provincia lombarda con i valori di alti di suolo consumato è Monza-Brianza, mentre quella con i valori più bassi è la provincia di Sondrio.

6.6 Esercizi Lab 5

6.6.1 Esercizio 1

Si considerino i dati contenuti nel file agriturismi.csv (disponibile in Mooodle nella cartella Dati) che riportano il numero di agriturismi per fascia altimetrica (montagna, collina, pianura) per l’anno 2022 (fonte: Istat).

Importare i dati in RStudio creando un oggetto di nome agr. Quali sono le sue dimensioni?
Fare il reshape dei dati da formato wide a formato long creando un nuovo dataframe denominato agrlong con 3 colonne (Regione, fascia_alt e n_agr). Quali sono le dimensioni di agrlong?
Calcolare il numero totale di agriturismi per ogni regione (considerando insieme tutte le fasce altimetriche). Quale regione ha il maggior numero totale di agriturismi?
Calcolare il numero totale di agriturismi per fascia altimetrica (considerando insieme tutte le regioni). Quale fascia altimetrica ha il maggior numero totale di agriturismi?
Si consideri la regione Trentino. Calcolare il numero totale di agriturismi condiziontamente alla fascia altimetrica. Commentare.
Utilizzare dei boxplot per rappresentare la distribuzione del numero di agriturismi per fascia altimetrica. Commentare. Calcolare inoltre i quartili con cui sono stati costruite le 3 scatole.
Considerando la fascia altimetrica collinare, quale regione risulta essere un outlier?
Considerando la fascia altimetrica di montagna, quali regioni risultano più agriturismi?