7 Lab 6 - 19/04/2024

In questa lezione vedremo:

come costruire una distribuzione bivariata e rappresentare graficamente due variabili qualitative,
come creare un grafico a dispersione che rappresenti due variabili quantitative,
come calcolare l’indice di correlazione per misurare la forza del legame lineare tra due variabili quantitative.

Verrà utilizzato un nuovo dataset prodotto da Istat riguardante le biblioteche presenti in Lombardia (si veda qui per maggiori dettagli). I dati sono disponibili nel file biblio.csv disponibile nella cartella Dati della pagina Moodle del corso. Le variabili a disposizione sono le seguenti:

provincia: provincia in cui si trova la biblioteca
comune: comune in cui si trova la biblioteca
denominaz: nome della biblioteca
tipo: tipo di biblioteca (1=pubblica, 2=privata)
nposti: numero di posti in biblioteca disponibili nel 2022 per la lettura e la consultazione
npc: numero di postazioni PC disponibili nel 2022 con accesso ad internet
wifi: disponibilità della rete wifi in biblioteca (1=sì, 2=no)
nutenti: accessi fisici totali che la biblioteca a registrato nel 2022
nlibri: patrimonio posseduto dalla biblioteca nel 2022
nlibrinew2022: quanta parte del patrimonio posseduto dalla biblioteca è stato aquisito nel 2022

Importiamo i dati come già descritto in Section 3.1 andando a creare un oggetto di nome biblio:

biblio = read.csv("./data/biblio.csv", stringsAsFactors = T)

L’opzione stringsAsFactors = T permette di considerare direttamente le variabili testuali presenti nel dataset come factor (ad esempio provincia, comune e denominazione).

Come prima cosa è necessario caricare il pacchetto tidyverse (come descritto in Section 4.2):

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.0
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.2     ✔ tidyr     1.3.0
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Con il comando glimpse andiamo a visionare le caratteristiche delle variabili contenute nel dataframe appena creato:

glimpse(biblio)

Rows: 1,294
Columns: 10
$ provincia   <fct> Bergamo                                           , Bergam…
$ comune      <fct> Adrara San Martino                                , Adrara…
$ denominaz   <fct> "Biblioteca comunale                                      …
$ tipo        <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 2, 2…
$ nposti      <int> 30, 34, 46, 150, 20, 35, 30, 24, 15, 50, 18, 22, 5, 20, 41…
$ npc         <int> 2, 1, 3, 2, 1, 0, 8, 2, 3, 4, 2, 3, 0, 0, 3, 0, 3, 0, 2, 0…
$ wifi        <int> 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1…
$ nutenti     <int> 1000, 52, 2589, 63416, 5600, 12000, 7000, 0, 530, 3000, 39…
$ nlibri      <int> 6492, 7093, 35432, 106640, 33163, 33614, 19162, 17875, 116…
$ nlibrinew22 <int> 339, 449, 1642, 2153, 1452, 2004, 644, 393, 719, 912, 863,…

Il dataset ha 1294 righe (come il numero di biblioteche in Lombardia per le quali sono stati raccolti tutti i dati) e 10 colonne (variabili).

Sono presenti 3 variabili qualitative sconnesse (provincia, comune e denominaz), 5 variabili quantitative (nposti, npc, nutenti, nlibri e nlibrinew22) e 2 variabili al momento quantitative (wifi e tipo) ma di natura qualitativa.

Il seguente codice permette di ottenere la distribuzione di frequenza della variabile provincia, ovvero di conteggiare quante volte ogni provincia si ripete nel dataframe, dandoci quindi l’informazione di quante biblioteche ci sono in ogni provincia:

biblio %>% 
  count(provincia)

                                            provincia   n
1  Bergamo                                            222
2  Brescia                                            206
3  Como                                               100
4  Cremona                                             77
5  Lecco                                               59
6  Lodi                                                47
7  Mantova                                             77
8  Milano                                             221
9     Monza e della Brianza                             1
10 Monza e della Brianza                               57
11 Pavia                                               83
12 Sondrio                                             40
13 Varese                                             104

biblio %>% 
  ggplot() +
  geom_bar(aes(provincia))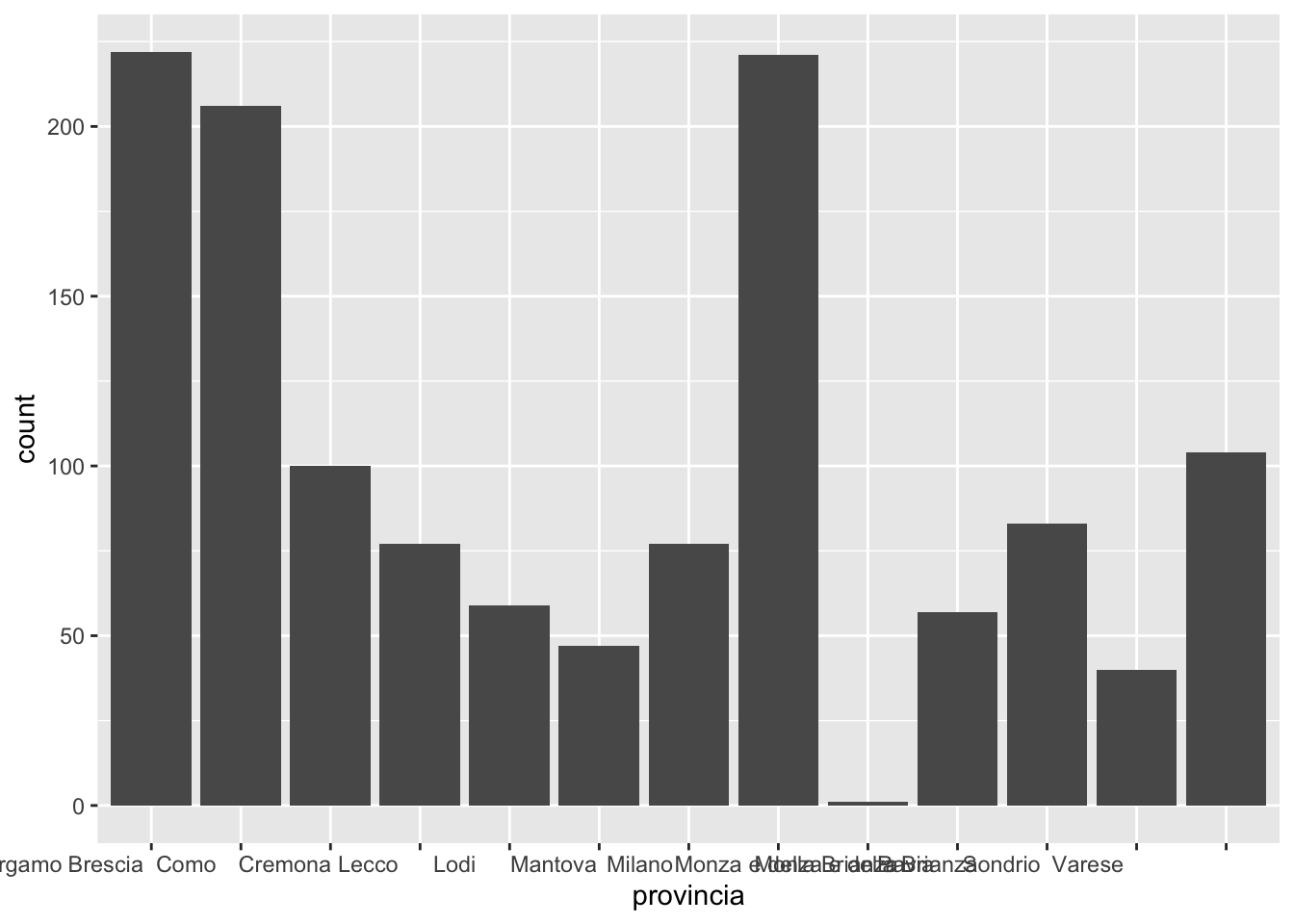

Si nota che accanto al nome di ogni provincia compariono spazi bianchi che creano problemi nella definizione dell’asse x del grafico. Andiamo quindi a rimuovere tutti gli eventuali spazi bianchi nel testo applicando la funzione str_trim a provincia (tramite il verbo mutate presentato in Section 4.4.2):

biblio = biblio %>% 
  mutate(provincia = str_trim(provincia)) 

glimpse(biblio)

Rows: 1,294
Columns: 10
$ provincia   <chr> "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Be…
$ comune      <fct> Adrara San Martino                                , Adrara…
$ denominaz   <fct> "Biblioteca comunale                                      …
$ tipo        <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 2, 2…
$ nposti      <int> 30, 34, 46, 150, 20, 35, 30, 24, 15, 50, 18, 22, 5, 20, 41…
$ npc         <int> 2, 1, 3, 2, 1, 0, 8, 2, 3, 4, 2, 3, 0, 0, 3, 0, 3, 0, 2, 0…
$ wifi        <int> 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1…
$ nutenti     <int> 1000, 52, 2589, 63416, 5600, 12000, 7000, 0, 530, 3000, 39…
$ nlibri      <int> 6492, 7093, 35432, 106640, 33163, 33614, 19162, 17875, 116…
$ nlibrinew22 <int> 339, 449, 1642, 2153, 1452, 2004, 644, 393, 719, 912, 863,…

# notare la scomparsa degli spazi bianchi nella 
# variabile provincia

Segue nuovamente il codice per il grafico a barre della variabile provincia dove questa volta le barre vengono ordinate (tramite la funzione fct_infreq) non in ordine alfabetico ma secondo le frequenze con cui ogni provincia si presenta:

biblio %>% 
  ggplot() +
  geom_bar(aes(fct_infreq(provincia))) +
  xlab("Provincia") +
  ylab("N. di biblioteche") +
  theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1)) # per ruotare il testo dell'asse x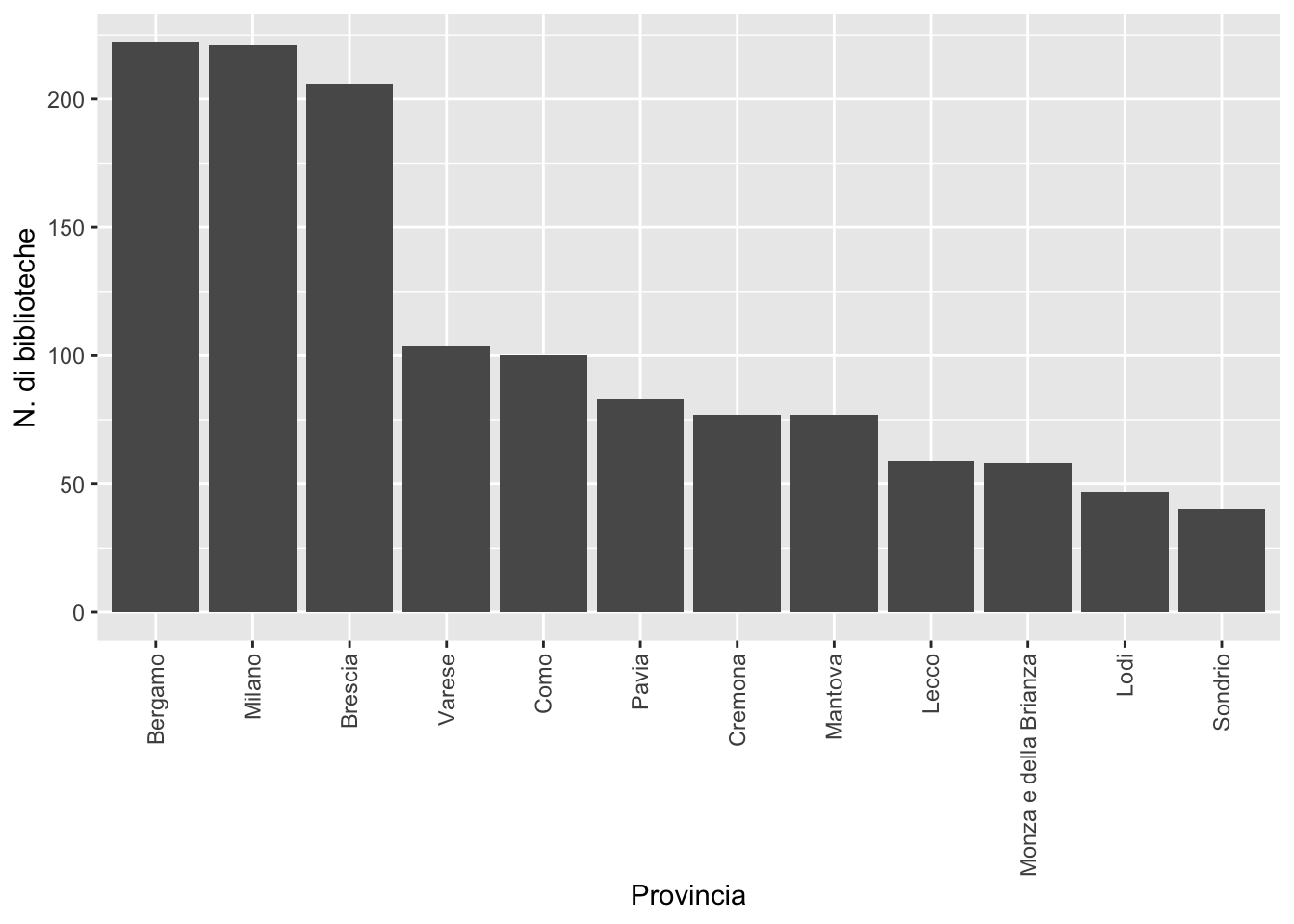

Il numero esatto del numero di biblioteche per provincia si ottiene come segue:

biblio %>% 
  count(provincia)

               provincia   n
1                Bergamo 222
2                Brescia 206
3                   Como 100
4                Cremona  77
5                  Lecco  59
6                   Lodi  47
7                Mantova  77
8                 Milano 221
9  Monza e della Brianza  58
10                 Pavia  83
11               Sondrio  40
12                Varese 104

Bergamo e Milano sono le province con il maggior numero di biblioteche, Sondrio quella con il minor numero.

7.1 Trasformare una variabile in fattore

Come anticipato, le variabili tipo e wifi sono al momento di tipo quantitativo pur essendo qualitative. Infatti, come riportato nella descrizione delle variabili, la seguente codifica vale per la variabile tipo: 1=pubblica, 2=privata:

biblio %>% 
  count(tipo)

  tipo    n
1    1 1189
2    2  105

Andiamo quindi a trasformare la variabile tipo in una variabile di tipo factor:

biblio = biblio %>% 
  mutate(tipo = factor(tipo,
          labels = c("pubblica","privata")))

biblio %>% 
  count(tipo)

      tipo    n
1 pubblica 1189
2  privata  105

Facciamo la stessa cosa con wifi sapendo che 1=sì, 2=no:

biblio %>%  count(wifi)

  wifi   n
1    1 983
2    2 311

biblio = biblio %>% 
  mutate(wifi = factor(wifi, 
                       labels = c("sì","no")))
biblio %>% 
  count(wifi)

  wifi   n
1   sì 983
2   no 311

Si noti che ora entrambe le variabile sono di tipo fct:

glimpse(biblio)

Rows: 1,294
Columns: 10
$ provincia   <chr> "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Bergamo", "Be…
$ comune      <fct> Adrara San Martino                                , Adrara…
$ denominaz   <fct> "Biblioteca comunale                                      …
$ tipo        <fct> pubblica, pubblica, pubblica, pubblica, pubblica, pubblica…
$ nposti      <int> 30, 34, 46, 150, 20, 35, 30, 24, 15, 50, 18, 22, 5, 20, 41…
$ npc         <int> 2, 1, 3, 2, 1, 0, 8, 2, 3, 4, 2, 3, 0, 0, 3, 0, 3, 0, 2, 0…
$ wifi        <fct> sì, no, sì, sì, sì, sì, sì, sì, sì, sì, sì, sì, no, sì, sì…
$ nutenti     <int> 1000, 52, 2589, 63416, 5600, 12000, 7000, 0, 530, 3000, 39…
$ nlibri      <int> 6492, 7093, 35432, 106640, 33163, 33614, 19162, 17875, 116…
$ nlibrinew22 <int> 339, 449, 1642, 2153, 1452, 2004, 644, 393, 719, 912, 863,…

7.2 Distribuzione bivariata di 2 variabili qualitative

Conosciamo già il comando count per ricavare la ditribuzione (univariata) di una variabile. E’ possibile utilizzarlo anche per ricavare la distribuzione bivariata di due variabili qualitative. Ad esempio il seguente codice

biblio %>% 
  count(wifi, tipo)

  wifi     tipo   n
1   sì pubblica 902
2   sì  privata  81
3   no pubblica 287
4   no  privata  24

ci restituisce la distribuzione congiunta delle due variabili. Si osserva che 902 sono le biblioteche in Lombardia pubbliche E con il wifi; 287 sono le biblioteche pubbliche E senza wifi. I numeri ottenuti potrebbero anche essere riportati in una tabella 2x2 (per un totale di 4 combinazioni di modalità) corredata di totali di riga e di colonna:

	Pubblica	Privata	TOT
No	287	24	311
Sì	902	81	983
TOT	1189	105	1294

Con il seguente codice calcoliamo le frequenze percentuali di ogni combinazione di modalità andando a dividere per il numero totale di biblioteche:

biblio %>% 
  count(wifi, tipo) %>% 
  mutate(perc = n/sum(n)*100)

  wifi     tipo   n      perc
1   sì pubblica 902 69.706337
2   sì  privata  81  6.259660
3   no pubblica 287 22.179289
4   no  privata  24  1.854714

Ad esmpio il 6.26% di tutte le biblioteche è privata E ha il wifi.

7.3 Rappresentazione grafica di due variabili qualitative

Andiamo ora a rappresentare insieme le due variabili qualitative andando a creare due barre (una per ogni modalità di wifi) ognuna divisa in due parti a seconda delle modalità di tipo (che verrà quindi utilizzata per definire il fill di ogni barra):

biblio %>% 
  ggplot() +
  geom_bar(aes(wifi, fill=tipo))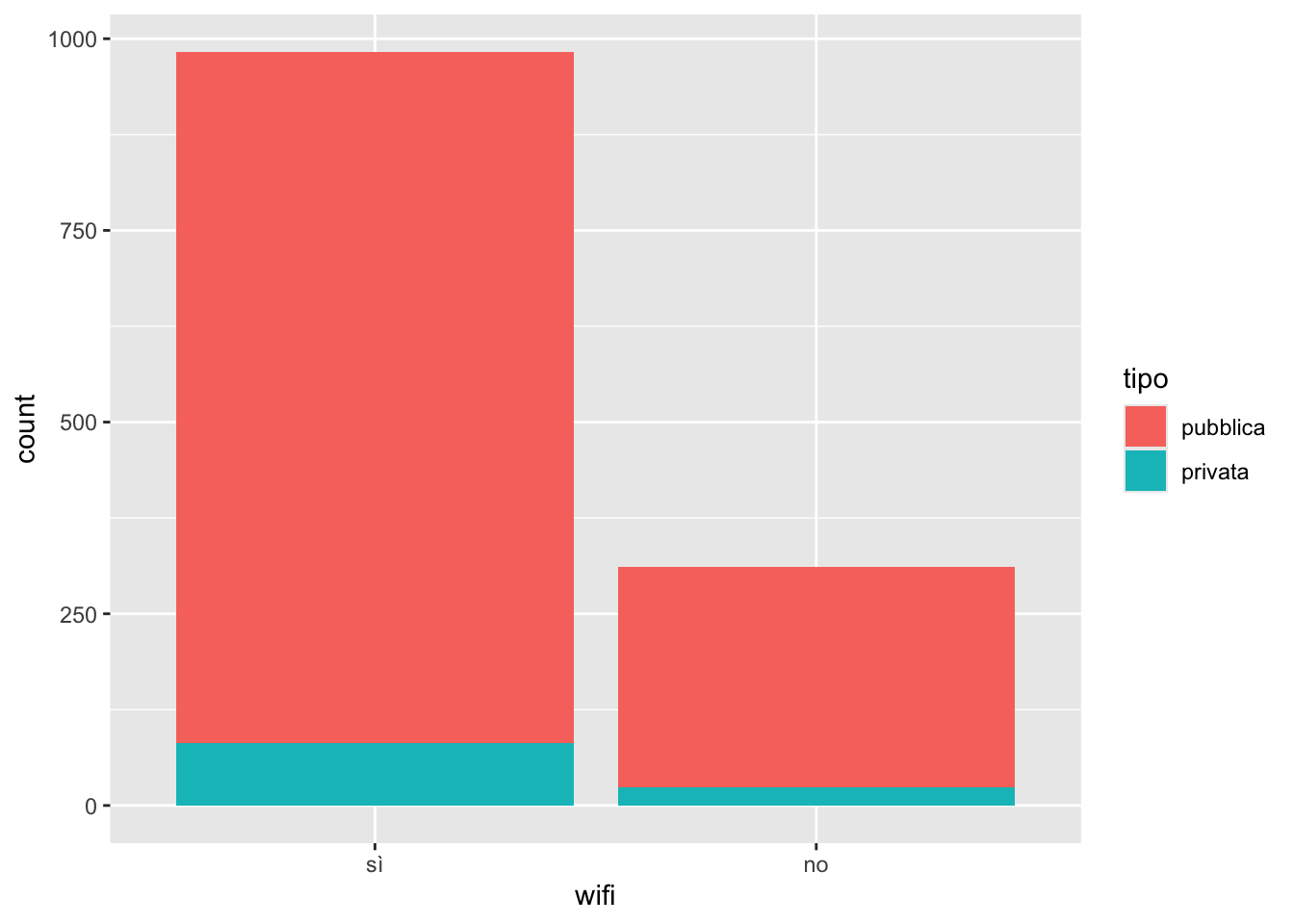

Si noti che le due barre hanno altezze diverse perchè il numero di biblioteche con o senza wifi è diverso (983 vs 311). E’ quindi difficile capire quanto pesa, all’interno di ogni barra, la parte relativa alle biblioteche private. Un’altra rappresentazione è possibile, con una diversa suddivisione delle barre in pubblica/privata (affiancata anzichè incolonnata):

biblio %>% 
  ggplot() +
  geom_bar(aes(wifi, fill=tipo),
           position = "dodge")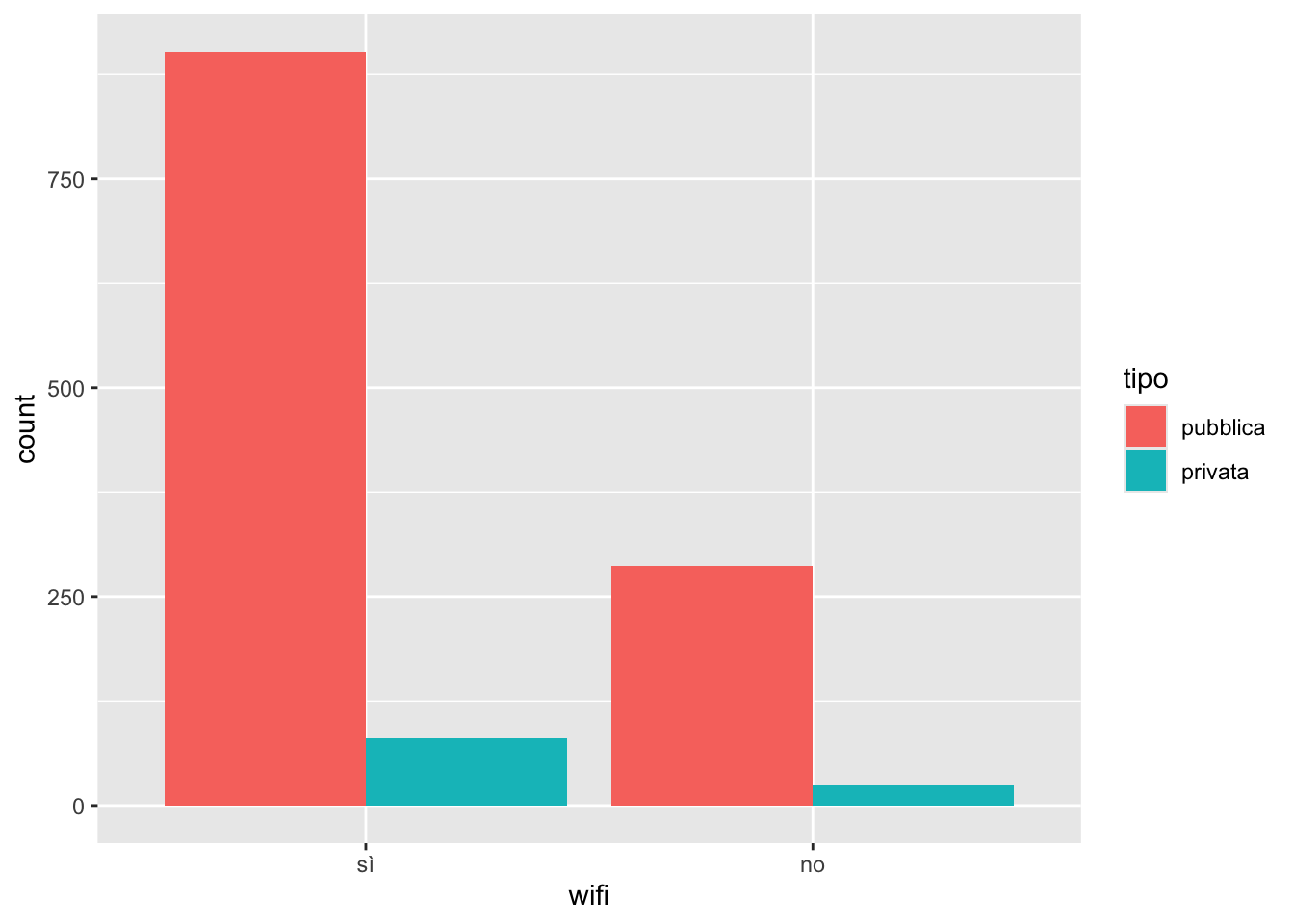

Anche in questo caso è difficile capire il peso della quota privata sul totale di pubblica+privata. Risulta invece conveniente la seguente rappresetazione:

biblio %>% 
  ggplot() +
  geom_bar(aes(wifi, fill=tipo),
           position = "fill")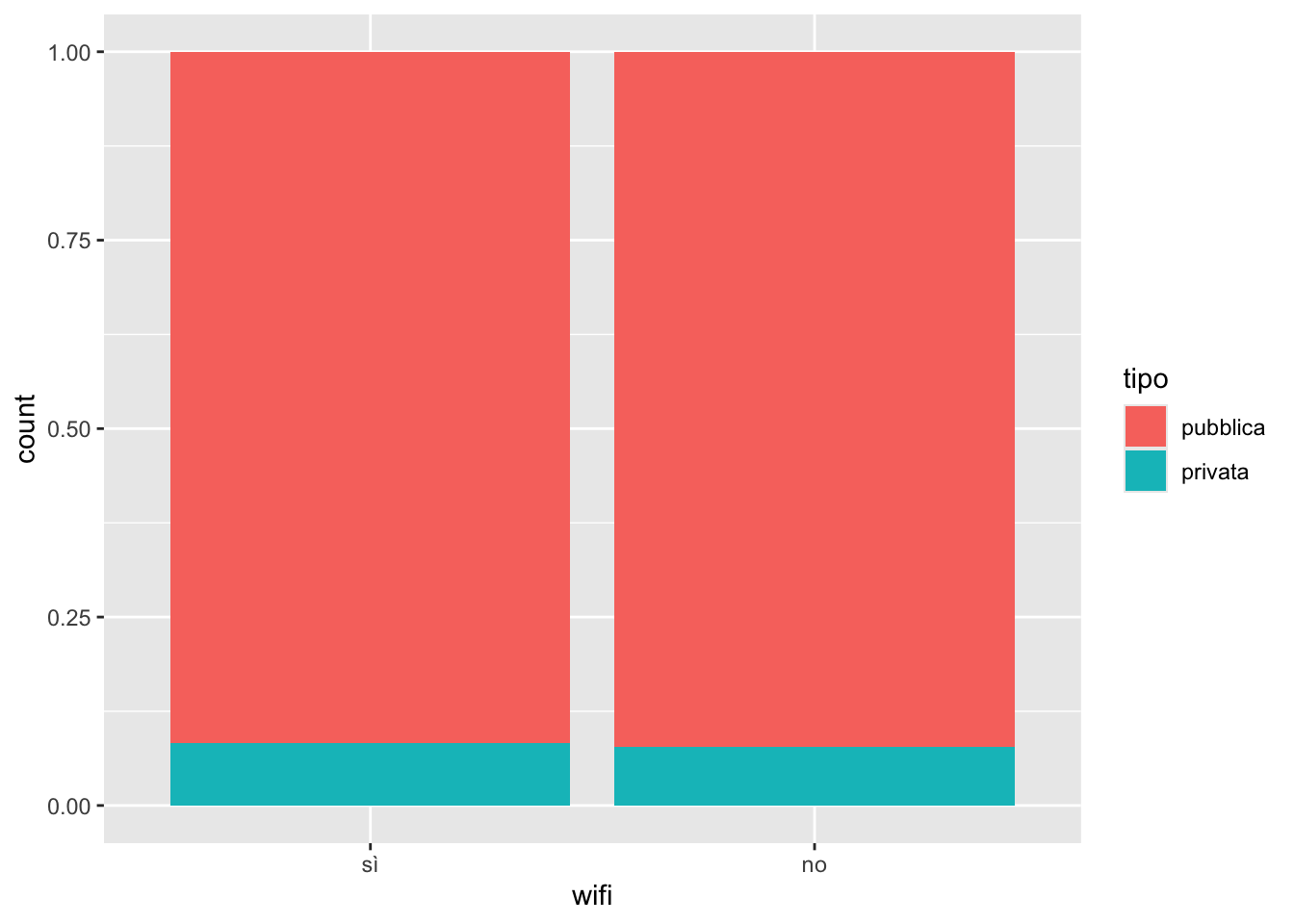

dove ognuna delle due barre rappresenta il 100% delle biblioteche con o senza wifi. Ogni barra è poi divisa in due parti per le modalità privata/pubblica. Con questa rappresentazione è chiaro che la quota di biblioteche private all’interno delle due modalità di wifi è di fatto molto simile (si vedano le due fette verdi). Per conoscere i numeri esatti del grafico si utilizza la funzione count come già fatto sopra ma andando a specificare un group_by che ci permetterà di calcolare le percentuali non sul numero totale di biblioteche (1294) ma sul numero di biblioteche in ogni categoria di wifi:

biblio %>% 
  group_by(wifi) %>% 
  count(wifi, tipo) %>% 
  mutate(perc = n/sum(n)*100)

# A tibble: 4 × 4
# Groups:   wifi [2]
  wifi  tipo         n  perc
  <fct> <fct>    <int> <dbl>
1 sì    pubblica   902 91.8 
2 sì    privata     81  8.24
3 no    pubblica   287 92.3 
4 no    privata     24  7.72

Il 91.8% delle biblioteche con il wifi è pubblica, mentre l’8.24% delle biblioteche con il wifi è privata (prima colonna nel grafico). Il 92.3% delle biblioteche senza il wifi è pubblica, mentre il 7.72% delle biblioteche senza il wifi è privata (seconda colonna nel grafico).

E’ possibile modificare la variabile secondo cui condizionare mettendo tipo invece di wifi:

biblio %>% 
  ggplot() +
  geom_bar(aes(tipo, fill=wifi),
           position = "fill")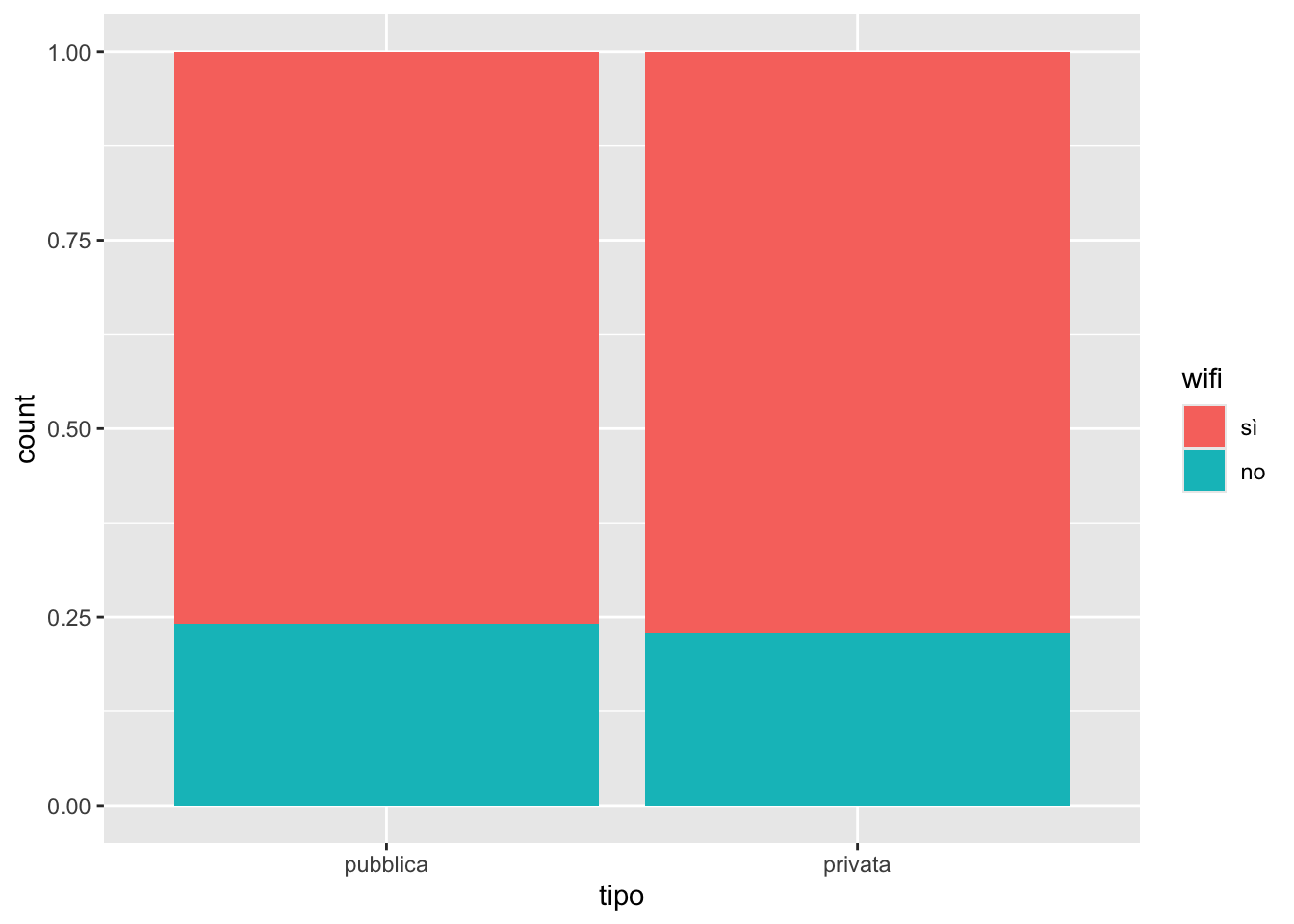

biblio %>% 
  group_by(tipo) %>% 
  count(wifi, tipo) %>% 
  mutate(perc = n/sum(n)*100)

# A tibble: 4 × 4
# Groups:   tipo [2]
  tipo     wifi      n  perc
  <fct>    <fct> <int> <dbl>
1 pubblica sì      902  75.9
2 pubblica no      287  24.1
3 privata  sì       81  77.1
4 privata  no       24  22.9

Il 75.9% delle biblioteche pubbliche ha il wifi, mentre il 24.1% delle biblioteche pubbliche non ha il wifi (prima colonna nel grafico). Il 77.1% delle biblioteche private ha il wifi, mentre il 22.9% delle biblioteche private non ha il wifi (seconda colonna nel grafico).

Decidere rispetto a quale variabile condizionare (quella sull’asse delle x) dipende dal punto di vista dell’analisi.

7.4 Grafico a dispersione

Il grafico a dispersione viene utilizzato per rappresentare graficamente due variabili quantitative (come ad esempio nposti e nutenti). Ogni pallino che apparirà nel grafico corrisponderà ad una biblioteca. La geometria da utilizzare è geom_point:

biblio %>% 
  ggplot() +
  geom_point(aes(nposti, nutenti))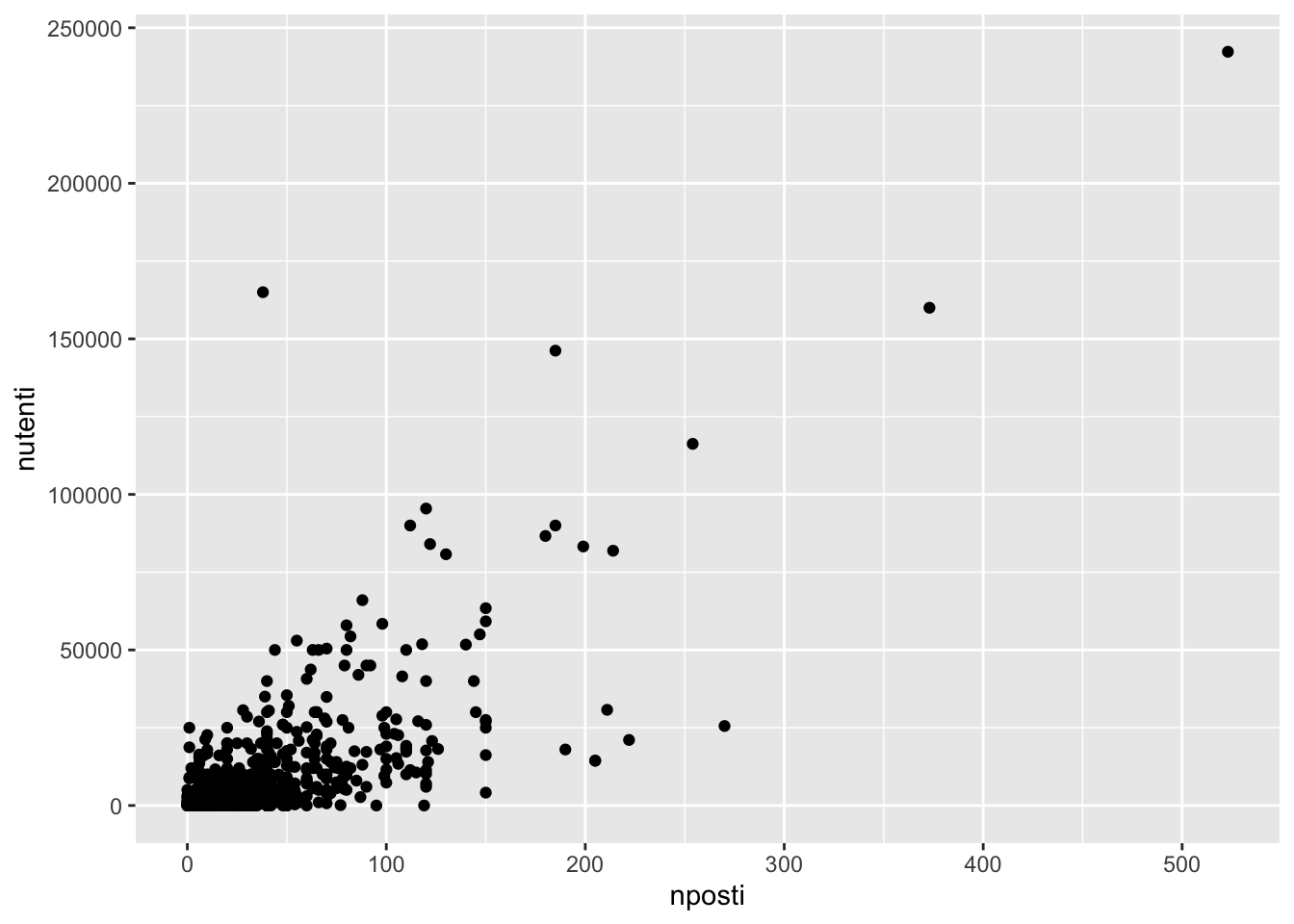

Solitamente la variabile sull’asse delle y (nutenti) si definisce variabile dipendente, mentre quella sull’asse delle x (nposti) variabile indipendente e si tende a studiare la y come una funzione di x. In questo caso si nota che a valori bassi di nposti corrispondono valori bassi di nutenti e a valori alti di nposti corrispondono valori alti di nutenti. In questo caso si parla di concordanza tra le due variabili. Tuttavia esistono anche delle eccezioni come biblioteche con pochi posti ma molti utenti o biblioteche con molti posti ma pochi utenti. La forza del legame tra due variabili si calcola con l’indice di correlazione \(\rho\) che si può calcolare come segue:

cor(biblio$nposti, biblio$nutenti)

[1] 0.7271796

Il valore positivo conferma la presenza di concordanza, il valore suggerisce un legame lineare medio-forte.

Andiamo ora a rappresentare graficamente le stesse variabili ma creando grafici a dispersione diversi per ogni provincia (tramite facet_wrap):

biblio %>% 
  ggplot() +
  geom_point(aes(nposti, nutenti)) +
  facet_wrap(~provincia, scales = "free")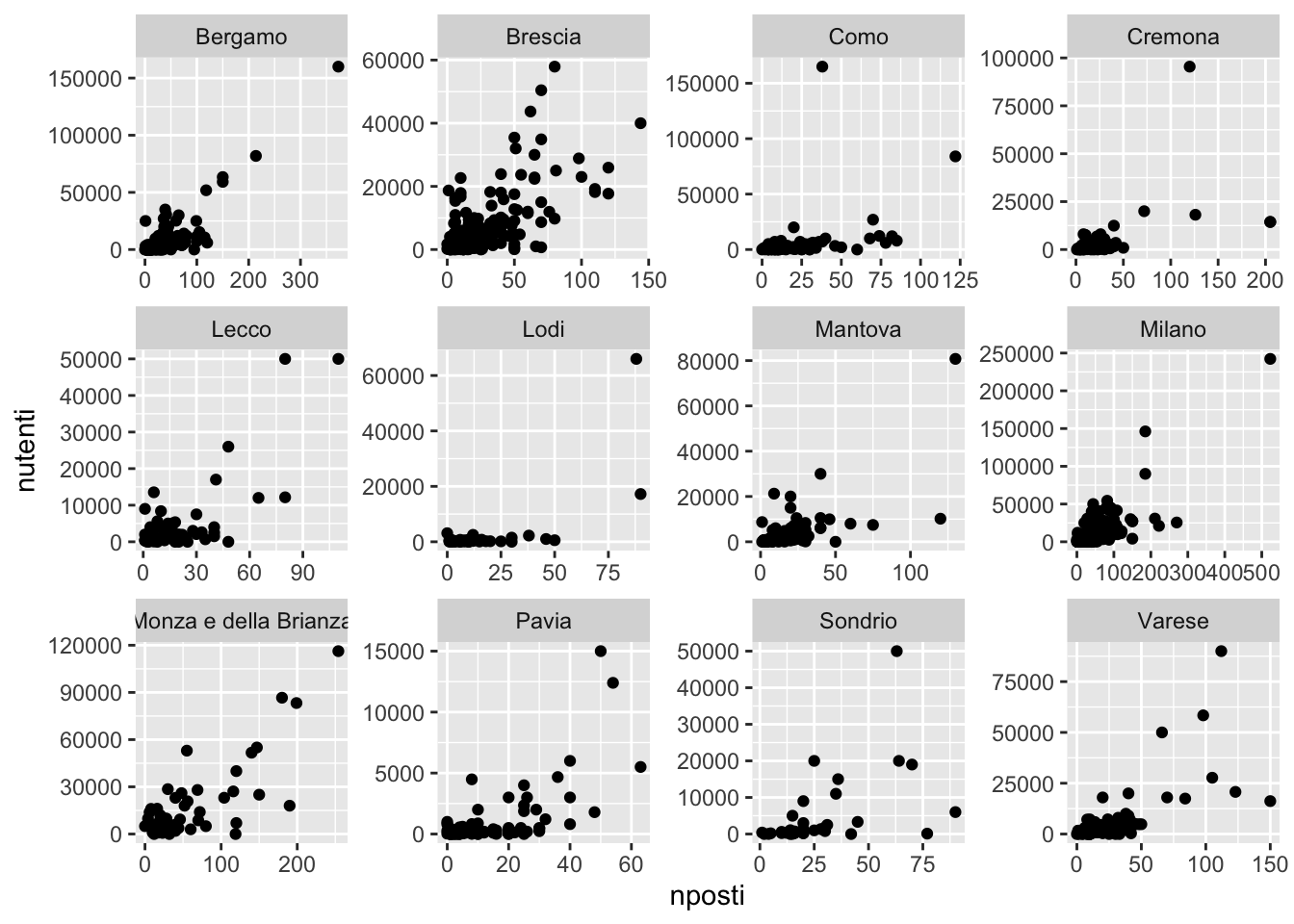

L’opzione scales = "free" permette ad ogni grafico di avere una diversa scala di valori per i due assi del grafico (altrimenti sarebbero uguali per tutti i grafici). Si nota sempre la presenza di concordanza tra le due variabili anche se le nuvole dei punti possono assumere una diversa forma e dispersione dei punti. E’ possibile calcolare la correlazione tra le due variabili separatamente per ogni provincia come segue:

biblio %>% 
  group_by(provincia) %>% 
  summarise(correl = cor(nposti,nutenti)) %>% 
  arrange(-correl)

# A tibble: 12 × 2
   provincia             correl
   <chr>                  <dbl>
 1 Bergamo                0.841
 2 Monza e della Brianza  0.780
 3 Milano                 0.778
 4 Lecco                  0.734
 5 Lodi                   0.698
 6 Varese                 0.695
 7 Mantova                0.658
 8 Brescia                0.651
 9 Pavia                  0.648
10 Cremona                0.523
11 Sondrio                0.518
12 Como                   0.404

Il verbo arrange permette di ordinare i risultati in senso crescente o decrescente (usando il meno) rispetto ai valori di correl. La provincia dove il legame lineare è più forte è Bergamo, mentre dove è più debole è Como (dove risulta positivo e medio basso).

Si noti che la correlazione fino ad ora è stata calcolata solo per una coppia di variabili (nposti e nutenti), ma può essere calcolata per qualsiasi coppia di variabili quantitative. Per calcolare tutte le possibili correlazioni con il minor codice possibile si procede come segue, dove il comando select_if(is.numeric) si occupa di selezionare solamente le variabili quantitative:

biblio %>% 
  select_if(is.numeric) %>% 
  cor()

               nposti       npc   nutenti    nlibri nlibrinew22
nposti      1.0000000 0.5297039 0.7271796 0.2586164   0.2902142
npc         0.5297039 1.0000000 0.4423519 0.1460934   0.1702358
nutenti     0.7271796 0.4423519 1.0000000 0.2586133   0.2739638
nlibri      0.2586164 0.1460934 0.2586133 1.0000000   0.6502499
nlibrinew22 0.2902142 0.1702358 0.2739638 0.6502499   1.0000000

Quello che si ottiene è la matrice di correlazione, una matrice quadrata le cui dimensioni sono date dal numero di variabili quantitative. Sulla diagonale sono presenti valori pari ad 1 (la correlazione tra una variabile e se stessa). Fuori dalla diagonale si trovano i valori di correlazione tra coppie di variabili. La matrice è simmetrica rispetto alla diagonale perchè in generale la correlazione tra \(X\) e \(Y\) è uguale alla correlazione tra \(Y\) e \(X\). Tutte le correlazioni sono positive (concordanza) anche se di valore diverso (quella maggiore si osserva tra nutenti e nposti, quella minore tra npc e nlibri).

7.5 Lab 6

7.5.1 Esercizio 1

Continuare ad utilizzare l’oggetto biblio creato nel Laboratorio 6.

Ricavare la distribuzione di frequenza e rappresentare graficamente la distribuzione della variabile tipo condizionatamente alla variabile provincia. In quale provincia si osserva la maggiore/minore presenza di biblioteche private?
Rappresentare graficamente i caratteri nutenti e nlibri. Colorare i puntini in funzione della provincia. Dopo aver calcolato la correlazione tra le due variabili commentare.
Trovare a quale biblioteca si riferiscono i 3 pallini in alto a sinistra nel grafico.
Rappresentare graficamente la distribuzione della variabile nutenti in funzione della provincia. Commentare.
Calcolare per ogni provincia il numero medio e mediano del numero di utenti insieme al coefficiente di variazione.
Rappresentare graficamente la distribuzione del carattere nlibrinew22 (nuovi libri acquistati nel 2022). Calcolare inoltre e commentare i quartili. Infine, identificare la biblioteca che nel 2022 ha comprato il maggior numero di libri.
Utilizzando nlibri e nlibrinew22 calcolare per ogni biblioteca quanti libri erano presenti nel 2021 (creare una nuova variabile nlibri21).
Calcolare quante biblioteche non hanno acquistato libri nuovi nel 2022 ed eliminarle (creare biblio2).
Usando biblio2 calcolare una nuova variabile (Delta) che calcoli l’incremento percentuale nel numero di libri dal 2021 al 2022 usando la seguente formula: \[ \Delta = \frac{y_{2022}-y_{2021}}{y_{2022}}\cdot 100 \]
Ricavare il valore minimo e massimo di Delta e capire a quale biblioteche corrispondono. Se i valori sono anomali eliminare le biblioteche.
Dopo aver eliminato i valori anomali di cui sopra, calcolare il valore di Delta medio.