4  Lab 3 - 15/03/2024

In questa lezione vedremo:

Verranno utilizzati i dati disponibili nel file DatiCom.csv che vengono quindi importati in R secondo quanto descritto in Section 3.1.

dati = read.csv("./data/DatiCom.csv")

Si tratta di un dataframe con 7900 righe (comuni) e 11 variabili la cui struttura è la seguente:

str(dati)
'data.frame':   7900 obs. of  11 variables:
 $ codreg  : int  1 1 1 1 1 1 1 1 1 1 ...
 $ codcom  : int  1001 1002 1003 1004 1006 1007 1008 1009 1010 1011 ...
 $ nomecom : chr  "Agli\x8f" "Airasca" "Ala di Stura" "Albiano d'Ivrea" ...
 $ sup     : num  13.2 15.7 46.3 11.7 17.9 ...
 $ pop     : int  2558 3681 465 1628 6280 251 16497 2012 479 810 ...
 $ zona_alt: int  3 5 1 3 3 1 3 3 1 1 ...
 $ alt     : int  315 257 1080 230 364 957 314 306 836 782 ...
 $ lito    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ isol    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ cost    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ urban   : int  2 3 3 3 2 3 2 3 3 3 ...

In particolare, la seguente è la definizione delle variabili:

4.1 Il pacchetto tidyverse

In generale un pacchetto di R è una collezione di funzioni, dati e documentazione che estende le capacità di R di base. La lista completa dei pacchetti di R è disponibile al link https://cran.r-project.org/web/packages/available_packages_by_name.html.

tidyverse è un insieme di pacchetti di R sviluppati appositamente per la data science (see Figure 4.1) e, in particolare, per manipolare, analizzare e rappresentare graficamente dati. Tutti i pacchetti dentro la collezione tidyverse condividono la stessa filosofia, struttura dei dati e sintassi del codice. Si veda qui per la pagine web di tidyverse e qui per il libro R for Data Science - edizione italiana.

Figure 4.1: Pacchetti contenuti nella collezione di tidyverse

Per vedere come installare un pacchetto si veda il paragrafo che segue.

4.2 Installare e caricare un pacchetto

Prima di iniziare ad utilizzare un pacchetto (ovvero le funzioni in esso contenute) è solitamente necessario seguire due passaggi:

  1. installare il pacchetto: questa procedura deve essere eseguita solamente una volta (a meno che decidiate di reinstallare R, di cambiare o resettare il computer). E’ come decidere di comprare una lampadina e di montarla (si veda Figure 4.2): questa azione viene fatta solamente una sola volta e non ogni volta che è necessario avere luce in una stanza.

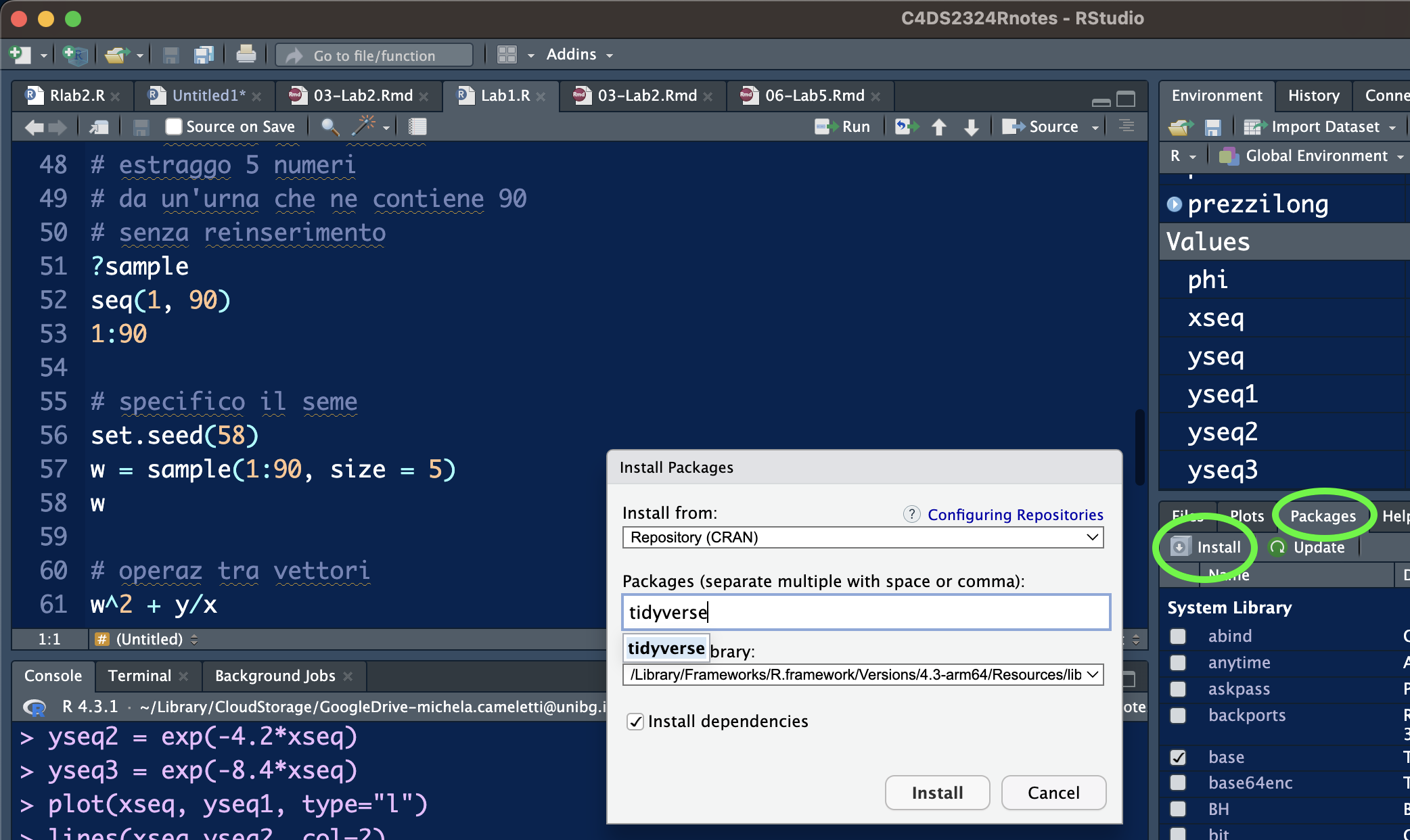
La procedura di installazione può essere fatta utilizzando il pannello in basso a destra di RStudio, tab Packages, icona “Install” (di fatto tramite il menù di RStudio si sta usando la funzione install.packages("...")).

  1. caricare il pacchetto: questa azione corrisponde all’azione di accendere con l’interrutore la luce in una stanza ogni qual volta sia necessario (si veda Figure 4.2). Allo stesso modo, un pacchetto può essere caricato più volte, ogni qual volta sia necessario utilizzare una delle funzioni incluse nel pacchetto.

Figure 4.2: Installare e caricare un pacchetto

Figure 4.3: Il menù di RStudio per installare nuovi pacchetti

Siamo ora interessati al pacchetto tidyverse (che in realtà è un insieme di pacchetto). Una volta che il pacchetto tidyverse è stato installato e caricato, è possibile utilizzare tutte le funzioni in esso contenute. Il caricamento di un pacchetto si esegue usando la funzione library:

library(tidyverse)
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.0
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.2     ✔ tidyr     1.3.0
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

4.3 Operatore pipe

La sintassi di tidyverse prevede l’uso dell’operatore pipe (%>%) che permette di scrivere in maniera molto intuitiva una sequenza di operazioni (vedere qui per più dettagli).

Si consideri una generica funzione di R denominata f con un unico argomento x. Di solito il seguente approccio (classico) viene utilizzato per utilizzare f:

f(x)

Un alternativa è data dall’operatore pipe %>% utilizzato con tidyverse. Funziona come segue, in maniera sequenziale:

x %>% f() 
#equivalente a f(x)

Di fatto, il pipe passa x come primo argomento della funzione f. La scorciatoia da tastiera che permette di digitare il pipe è CTRL/CMD Shift M (shift è il tasto per il maiuscolo).

Facciamo ora qualche esempio con il pipe utilizzando un vettore di 5 dati:

x = c(11, 19, 3, 7, 12)

x
[1] 11 19  3  7 12

Siamo ora interessati a calcolare il logaritmo naturale dei numeri in x. Con l’approccio standard di R utilizziamo il seguente codice:

log(x)
[1] 2.397895 2.944439 1.098612 1.945910 2.484907

mentre con il pipe

x %>% 
  log()
[1] 2.397895 2.944439 1.098612 1.945910 2.484907

dove x è utilzzato come primo argomento della funzione log. E’ anche possibile specificare un secondo argomento, come ad esempio la base (base) del logaritmo (ad esempio 5). In questo caso x %>% f(y) coincide con f(x,y).

#approccio standard
log(x, base=5) 
[1] 1.4898961 1.8294828 0.6826062 1.2090620 1.5439593
#approccio con pipe
x %>% 
  log(base=5)
[1] 1.4898961 1.8294828 0.6826062 1.2090620 1.5439593

Vogliamo ora, dopo aver calcolato il logaritmo, arrotondare tutti i numeri a due decimali. Questo richiede l’utilizzo di due funzioni (log e round):

# approccio standard
round(log(x, base = 5), digits = 2)
[1] 1.49 1.83 0.68 1.21 1.54
#approccio con pipe
x %>% 
  log(base = 5)%>%
  round(digits = 2)
[1] 1.49 1.83 0.68 1.21 1.54

Aggiungiamo ora un altro passaggio. Dopo aver arrotondiamo i 5 numeri ne facciamo la somma:

# approccio standard
sum(round(log(x, base = 5), digits = 2))
[1] 6.75
# approcci con pipe
x %>% 
  log(base = 5) %>% 
  round(digits = 2) %>% 
  sum 
[1] 6.75

Il risultato è uno scalare.

4.4 Prime funzioni (verbi) di tidyverse

Andiamo ora a lavorare con l’oggetto (dataframe) dati creato precedentemente. In particolare, andremo ad utilizzare le principali funzioni dal pacchetto tidyverse (usando l’operatore pipe %>%).

4.4.1 Distribuzione di frequenza con count

Per calcolare la distribuzione di frequenza (si veda anche Section 3.2) si può utilizzare la funzione count. Ad esempio, per la variabile zona_alt si procede come segue:

dati %>% 
  count(zona_alt)
  zona_alt    n
1        1 2370
2        2  117
3        3 2530
4        4  785
5        5 2098

Viene restituita una tabella con 5 righe (il numero di modalità di zona_alt) e due colonne: quella con le modalità e quella con le frequenze assolute (si noti il nome n della seconda colonna, scelto in automatico dalla funzione count). La moda della distribuzione è la modalità 3 (Collina Interna) in quanto ad essa è associata la frequenza maggiore.

4.4.2 mutate: per creare nuove variabili

La funzione mutate permette di creare una nuova colonna/variabile nel dataframe ottenuta come trasformazione di una delle variabili esistenti.

Si voglia ad esempio definire una nuova variabile (denominata altkm) data dall’altitudine alt espressa in kilometri anzichè metri. Si procede come segue:

dati = dati %>% 
  mutate(altkm = alt/1000)

Si noti che utilizzano dati= ... si va a sovrascrivere il vecchio dataframe. La nuova versione di dati avrà quindi una nuova colonna:

str(dati)
'data.frame':   7900 obs. of  12 variables:
 $ codreg  : int  1 1 1 1 1 1 1 1 1 1 ...
 $ codcom  : int  1001 1002 1003 1004 1006 1007 1008 1009 1010 1011 ...
 $ nomecom : chr  "Agli\x8f" "Airasca" "Ala di Stura" "Albiano d'Ivrea" ...
 $ sup     : num  13.2 15.7 46.3 11.7 17.9 ...
 $ pop     : int  2558 3681 465 1628 6280 251 16497 2012 479 810 ...
 $ zona_alt: int  3 5 1 3 3 1 3 3 1 1 ...
 $ alt     : int  315 257 1080 230 364 957 314 306 836 782 ...
 $ lito    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ isol    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ cost    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ urban   : int  2 3 3 3 2 3 2 3 3 3 ...
 $ altkm   : num  0.315 0.257 1.08 0.23 0.364 0.957 0.314 0.306 0.836 0.782 ...

Si ritorni ora alla distribuzione di frequenza calcola precedentemente per zona_alt:

dati %>% 
  count(zona_alt)
  zona_alt    n
1        1 2370
2        2  117
3        3 2530
4        4  785
5        5 2098

e si voglia aggiungere a questa tabella (dataframe) - con mutate - una nuova colonna data dalle frequenze percentuali (si veda Section 3.2) arrotondate a un decimale:

dati %>% 
  count(zona_alt) %>% 
  mutate(perc = n/sum(n)*100) %>% 
  mutate(perc = round(perc,1))
  zona_alt    n perc
1        1 2370 30.0
2        2  117  1.5
3        3 2530 32.0
4        4  785  9.9
5        5 2098 26.6

Si noti la possibilità di concatenare più operazioni utilizzando l’operatore %>%.

4.4.3 select: per selezionare le variabili

La funzione select permette di selezionare una o più variabili dal dataframe. Ad esempio il seguente codice:

dati %>% 
  select(pop) %>% 
  head()
   pop
1 2558
2 3681
3  465
4 1628
5 6280
6  251

seleziona solamente la colonna pop tra tutte quelle disponibili. L’utilizzo della funzione head() serve solamente a mostrare le prime 6 righe dell’output (che altrimenti sarebbe composto da quasi 8000 righe). Per selezionare eventualmente più variabili esse vanno specificate separate da virgola. Ad esempio:

dati %>% 
  select(pop, lito, cost) %>% 
  head()
   pop lito cost
1 2558    0    0
2 3681    0    0
3  465    0    0
4 1628    0    0
5 6280    0    0
6  251    0    0

Se le variabili sono consecutive si può utilizzare il :, ad esempio:

dati %>% 
  select(sup:isol) %>% #tutte le variabili da sup a isol
  head()
    sup  pop zona_alt  alt lito isol
1 13.15 2558        3  315    0    0
2 15.74 3681        5  257    0    0
3 46.33  465        1 1080    0    0
4 11.73 1628        3  230    0    0
5 17.88 6280        3  364    0    0
6  5.63  251        1  957    0    0

Infine, è anche possibile utilizzare select con il segno - per selezionare tutte le variabili tranne alcune. Si voglia ora ad esempio NON selezionare altkm eliminandola definitivmente dal dataframe dati:

dati = dati %>% 
  select(-altkm)
str(dati) #altkm non c'è più
'data.frame':   7900 obs. of  11 variables:
 $ codreg  : int  1 1 1 1 1 1 1 1 1 1 ...
 $ codcom  : int  1001 1002 1003 1004 1006 1007 1008 1009 1010 1011 ...
 $ nomecom : chr  "Agli\x8f" "Airasca" "Ala di Stura" "Albiano d'Ivrea" ...
 $ sup     : num  13.2 15.7 46.3 11.7 17.9 ...
 $ pop     : int  2558 3681 465 1628 6280 251 16497 2012 479 810 ...
 $ zona_alt: int  3 5 1 3 3 1 3 3 1 1 ...
 $ alt     : int  315 257 1080 230 364 957 314 306 836 782 ...
 $ lito    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ isol    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ cost    : int  0 0 0 0 0 0 0 0 0 0 ...
 $ urban   : int  2 3 3 3 2 3 2 3 3 3 ...

4.4.4 case_when: ricodifica di una variabile

La variabile zona_alt, come visto precedentemente, assume come categorie i valori interi da 1 a 5. Come specificato all’inizio di questa lezione, in realtà questa è una variabile qualitativa con le seguenti modalità: 1=Montagna interna; 2=Montagna litoranea; 3=Collina interna; 4=Collina litoranea; 5=Pianura. Procediamo quindi ora alla ricodifica di zona_alt usando la funzione mutate (creiamo una nuova variabile zona_alt2) abbinata a case_when. Si procede come segue:

dati = dati %>% 
  mutate(zona_alt2 = case_when(
    zona_alt == 1 ~ "Montagna interna",
    zona_alt == 2 ~ "Montagna lit.",
    zona_alt == 3 ~ "Collina interna",
    zona_alt == 4 ~ "Collina lit.",
    zona_alt == 5 ~ "Pianura"
  ))

Alla sinistra della tilde ~ vengono specificate le categorie numeriche della variabile zona_alt (attenzione il simbolo == significa “esattamente uguale a”), mentre a destra della tilde le nuove categorie (stringhe di testo tra virgolette) della nuova variabile zona_alt2. Per verificare che tutto sia corretto possiamo calcolare la nuova distribuzione di frequenza:

dati %>% 
  count(zona_alt2)
         zona_alt2    n
1  Collina interna 2530
2     Collina lit.  785
3 Montagna interna 2370
4    Montagna lit.  117
5          Pianura 2098

4.4.5 summarise: per calcolare le statistiche descrittive

La funzione di tidyverse denominata summarise ci permette di calcolare delle statistiche descrittive per ciascuna colonna (variabile). Ad esempio il seguente codice calcola la media e la mediana dell’altitudine si procede come segue:

dati %>% 
  summarise(mean(alt), median(alt))
  mean(alt) median(alt)
1  354.6885         289

E’ possibile anche calcolare statistiche descrittive condizionatamente alle categorie di una variabile qualitativa come zona_alt2:

dati %>% 
  group_by(zona_alt2) %>% 
  summarise(mean(alt), median(alt))
# A tibble: 5 × 3
  zona_alt2        `mean(alt)` `median(alt)`
  <chr>                  <dbl>         <dbl>
1 Collina interna        339.           318 
2 Collina lit.           205.           180 
3 Montagna interna       653.           638.
4 Montagna lit.          298.           300 
5 Pianura                 96.1           74

Come ci si aspetta, l’altitudine media (e mediana) per i comuni di montagna interna (653 metri) è maggiore dell’altitudine media dei comuni di pianura (96.1 metri).

4.5 Esercizi Lab 3

4.5.1 Esercizio 1

Si consideri nuovamente il dataframe dati relativo ai dati dei comuni italiani, già considerato per il Lab 3. Caricare la libreria tidyverse.

  1. Creare una nuova variabile denominata dens che rappresenta la densità di popolazione. Essa è data dal rapporto tra la popolazione residente e la superficie del comune.

  2. Creare una nuova variabile urban2 andando a ricodificare la variabile urban secondo le seguenti categorie: 1=Zone densamente popolate; 2=Zone a densità intermedia; 3=Zone scarsamente popolate.

  3. Ricavare la distribuzione di frequenza della variabile urban2 usando anche le frequenze percentuali. Quale è la moda della distribuzione?

  4. Calcolare la densità di popolazione media dei comuni italiani usando dens. Commentare.

  5. Calcolare la densità di popolazione media dei comuni italiani usando dens, condizionatamente alle categorie di urban2. Commentare.

  6. Creare un nuovo dataframe smalldati che contiene solamente le colonne codcom, sup e pop.